题目内容
【题目】已知
，
分别为双曲线
的左、右焦点，点P是以
为直径的圆与C在第一象限内的交点，若线段
的中点Q在C的渐近线上，则C的两条渐近线方程为__________．
【答案】y＝±2x
【解析】
求得双曲线的渐近线方程，由圆的性质可得PF1⊥PF2，由三角形的中位线定理可得PF1⊥OQ，OQ的方程设为bx+ay＝0，运用点到直线的距离公式可得F1（﹣c，0）到OQ的距离，结合双曲线的定义可得b＝2a，进而双曲线的渐近线方程．
双曲线
的渐近线方程为y＝±
x，
点P是以F1F2为直径的圆与C在第一象限内的交点，可得PF1⊥PF2，
线段PF1的中点Q在C的渐近线，可得OQ∥PF2，
且PF1⊥OQ，OQ的方程设为bx+ay＝0，
可得F1（﹣c，0）到OQ的距离为
b，
即有|PF1|＝2b，|PF2|＝2|OQ|＝2a，
由双曲线的定义可得|PF1|﹣|PF2|＝2b﹣2a＝2a，
即b＝2a，
所以双曲线的渐近线方程为y＝±2x．
故答案为：y＝±2x．
阅读快车系列答案【题目】某校为了了解学生对消防知识的了解情况，从高一年级和高二年级各选取100名同学进行消防知识竞赛.下图（1）和图（2）分别是对高一年级和高二年级参加竞赛的学生成绩按
分组，得到的频率分布直方图.
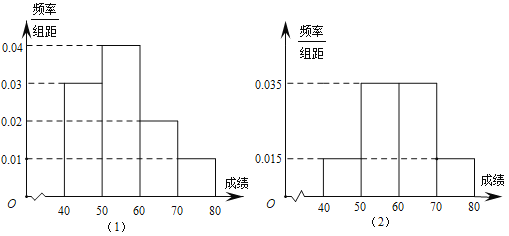
（1）请计算高一年级和高二年级成绩小于60分的人数；
（2）完成下面
列联表，并回答：有多大的把握可以认为“学生所在的年级与消防常识的了解存在相关性”？
成绩小于60分人数 | 成绩不小于60分人数 | 合计 | |
高一 | |||
高二 | |||
合计 |
附：临界值表及参考公式：
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某商场举行优惠促销活动，顾客仅可以从以下两种优惠方案中选择一种，
方案一：每满200元减50元；
方案二：每满200元可抽奖一次．具体规则是依次从装有3个红球、l个白球的甲箱，装有2个红球、2个白球的乙箱，以及装有1个红球、3个白球的丙箱中各随机摸出1个球，所得结果和享受的优惠如下表：（注：所有小球仅颜色有区别）
红球个数 | 3 | 2 | 1 | 0 |
实际付款 | 半价 | 7折 | 8折 | 原价 |
（1）若两个顾客都选择方案二，各抽奖一次，求至少一个人获得半价优惠的概率；
（2）若某顾客购物金额为320元，用所学概率知识比较哪一种方案更划算？
【题目】中国大学先修课程，是在高中开设的具有大学水平的课程，旨在让学有余力的高中生早接受大学思维方式、学习方法的训练，为大学学习乃至未来的职业生涯做好准备.某高中开设大学先修课程已有两年，两年共招收学生2000人，其中有300人参与学习先修课程，两年全校共有优等生200人，学习先修课程的优等生有60人.这两年学习先修课程的学生都参加了考试，并且都参加了某高校的自主招生考试（满分100分），结果如下表所示：
分数 |
|
|
|
|
|
人数 | 20 | 55 | 105 | 70 | 50 |
参加自主招生获得通过的概率 | 0.9 | 0.8 | 0.6 | 0.5 | 0.4 |
（1）填写列联表，并画出列联表的等高条形图，并通过图形判断学习先修课程与优等生是否有关系，根据列联表的独立性检验，能否在犯错误的概率不超过0.01的前提下认为学习先修课程与优等生有关系？
优等生 | 非优等生 | 总计 | |
学习大学先修课程 | |||
没有学习大学先修课程 | |||
总计 |
（2）已知今年有150名学生报名学习大学先修课程，以前两年参加大学先修课程学习成绩的频率作为今年参加大学先修课程学习成绩的概率.
①在今年参与大学先修课程的学生中任取一人，求他获得某高校自主招生通过的概率；
②设今年全校参加大学先修课程的学生获得某高校自主招生通过的人数为
，求
.
参考数据：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式：
，其中
.
