题目内容
(12分)已知函数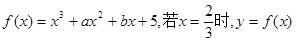 有极值,且曲线
有极值,且曲线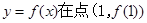 处的切线斜率为3.
处的切线斜率为3.
(1)求函数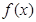 的解析式;
的解析式;
(2)求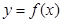 在
在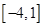 上的最大值和最小值.
上的最大值和最小值.
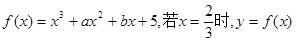 有极值,且曲线
有极值,且曲线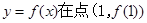 处的切线斜率为3.
处的切线斜率为3.(1)求函数
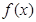 的解析式;
的解析式;(2)求
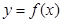 在
在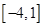 上的最大值和最小值.
上的最大值和最小值.(1)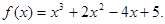 (2)在[-4,.m 1]上的最大值为13,最小值为-11。
(2)在[-4,.m 1]上的最大值为13,最小值为-11。
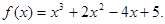 (2)在[-4,.m 1]上的最大值为13,最小值为-11。
(2)在[-4,.m 1]上的最大值为13,最小值为-11。试题分析:(1)先求函数f(x)=x3+ax2+bx+5的导函数,再由x=
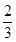 时,y=f(x)有极值,列一方程,曲线y=f(x)在点f(1)处的切线斜率为3,列一方程,联立两方程即可得a、b值
时,y=f(x)有极值,列一方程,曲线y=f(x)在点f(1)处的切线斜率为3,列一方程,联立两方程即可得a、b值(2)先求函数f(x)=x3+ax2+bx+5的导函数,再解不等式得函数的单调区间,最后列表列出端点值f(-4),f(1)及极值,通过比较求出y=f(x)在[-4,1]上的最大值和最小值。
解:(1)
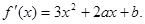
由题意,得
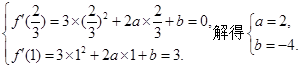
所以,
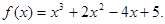
(2)由(1)知
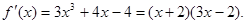 ,
,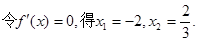
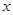 | -4 | (-4,-2) | -2 | 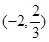 | 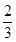 | 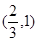 | 1 |
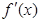 | | + | 0 | - | 0 | + | |
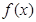 | |   | 极大值 |   | 极小值 |   | |
| 函数值 | -11 | | 13 | | 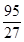 | | 4 |
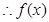 在[-4,.m 1]上的最大值为13,最小值为-11。考点:
在[-4,.m 1]上的最大值为13,最小值为-11。考点:点评:解决该试题的关键是理解导数的读好对于函数单调性的影响,导数大于零得到的区间为增区间,导数小于零得到的区间为减区间,进而判定单调性得到最值。

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
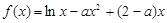 .
.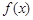 的单调性;
的单调性;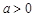 ,证明:当
,证明:当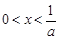 时,
时,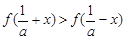 ;
;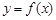 的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,证明:
的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,证明: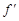 (x0)<0.(本题满分14分)
(x0)<0.(本题满分14分) 在定义域
在定义域 内可导,其图象如图所示,记
内可导,其图象如图所示,记 ,则满足
,则满足 的实数
的实数 的范围是 .
的范围是 . 
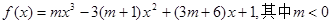 。
。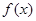 的单调增区间是(0,1)求m的值。
的单调增区间是(0,1)求m的值。 时,函数
时,函数 的图象上任意一点的切线斜率恒大于3m,求m的取值范围。
的图象上任意一点的切线斜率恒大于3m,求m的取值范围。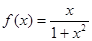 ,则
,则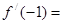

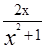 - 2的极值.
- 2的极值.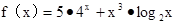 ②
② 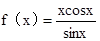
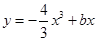 有三个单调区间,则
有三个单调区间,则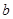 的取值范围是 .
的取值范围是 .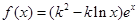 (
(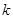 为非零常数,
为非零常数,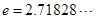 是自然对数的底数),曲线
是自然对数的底数),曲线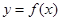 在点
在点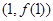 处的切线与
处的切线与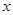 轴平行.
轴平行.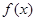 的单调性;
的单调性;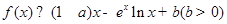 , 求
, 求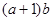 的最大值.
的最大值.