题目内容
15.圆(x-3)2+(y+1)2=3关于直线x+2y-3=0对称的圆的方程为(x-$\frac{19}{5}$)2+(y-$\frac{3}{5}$)2=3.分析 求出圆的圆心(3,-1)关于直线x+2y-3=0的对称点的坐标,即可得出圆(x-3)2+(y+1)2=3关于直线x+2y-3=0对称的圆的方程.
解答 解:设圆的圆心(3,-1)关于直线x+2y-3=0的对称点的坐标是(a,b),
则$\left\{\begin{array}{l}\frac{b+1}{a-3}×(-\frac{1}{2})=-1\\ \frac{3+a}{2}+2×\frac{b-1}{2}-3=0\end{array}\right.$,所以a=$\frac{19}{5}$,b=$\frac{3}{5}$,
所以圆的圆心(3,-1)关于直线x+2y-3=0的对称点的坐标是($\frac{19}{5}$,$\frac{3}{5}$),
所以圆(x-3)2+(y+1)2=1关于直线x+2y-3=0对称的圆的方程是(x-$\frac{19}{5}$)2+(y-$\frac{3}{5}$)2=3.
故答案为:(x-$\frac{19}{5}$)2+(y-$\frac{3}{5}$)2=3.
点评 本题考查圆的标准方程,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
5.已知平面α⊥β,α∩β=m,n?β,则“n⊥m”是“n⊥α”成立的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
6.双曲线$\frac{x^2}{10}-\frac{y^2}{2}$=1的焦距为( )
| A. | 2$\sqrt{3}$ | B. | 4$\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{3}$ |
10.长方体的一个顶点上三条棱长分别为2,4,5,则它的表面积为( )
| A. | 22 | B. | 40 | C. | 45 | D. | 76 |
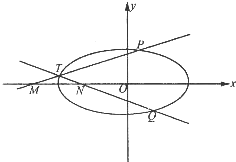 如图所示,椭圆C的离心率为$\frac{\sqrt{3}}{2}$,以坐标原点O为圆心,椭圆C的短半轴长为半径的圆与直线y=$\sqrt{3}$x+2相切.
如图所示,椭圆C的离心率为$\frac{\sqrt{3}}{2}$,以坐标原点O为圆心,椭圆C的短半轴长为半径的圆与直线y=$\sqrt{3}$x+2相切.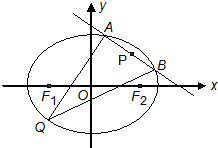 如图所示,已知椭圆C的方程为$\frac{x^2}{2}+{y^2}$=1,F1,F2分别是椭圆C的左、右焦点,直线AB:y=kx+m(k<0)与椭圆C交于不同的A,B两点.
如图所示,已知椭圆C的方程为$\frac{x^2}{2}+{y^2}$=1,F1,F2分别是椭圆C的左、右焦点,直线AB:y=kx+m(k<0)与椭圆C交于不同的A,B两点.