题目内容
16. 如图,在三棱锥P-ABC中,AC⊥BC,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E、F分别是PC,PB的中点,记平面AEF与平面ABC的交线为直线l.
如图,在三棱锥P-ABC中,AC⊥BC,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E、F分别是PC,PB的中点,记平面AEF与平面ABC的交线为直线l.(Ⅰ)求证:直线l⊥平面PAC;
(Ⅱ)直线l上是否存在点Q,使直线PQ分别与平面AEF、直线EF所成的角互余?若存在,求出|AQ|的值;若不存在,请说明理由.
分析 (I)利用中位线,直线平面的平行问题得出l∥BC,根据直线平面的垂直问题得出BC⊥平面PAC,即可得出直线l⊥平面PAC.
(II)建立坐标系得出平面AEF的法向量,cos<$\overrightarrow{CP}$,$\overrightarrow{PQ}$>,cos<$\overrightarrow{PQ}$,$\overrightarrow{EF}$>,直线平面,直线的夹角的关系求解即可,sinα=|$\frac{-1}{\sqrt{{y}^{2}+4}}$|,cosβ=|$\frac{-1+4y}{3\sqrt{{y}^{2}+4}}$|,sinα=cosβ.
解答 (I)证明:∵E,F分别为PB,PC中点,
∴BC∥EF,
又EF⊆平面EFA,BC?平面EFA,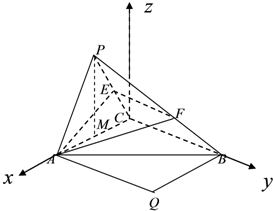
∴BC∥平面EFA
又BC⊆平面ABC,平面EFA∩平面ABC=l,
∴l∥BC.
∵AC⊥BC,
∴EF⊥BC,
∵PA=PC=AC=2,
∴AE⊥PC,
∵AC⊥BC,平面PAC⊥平面ABC,
∴BC⊥平面PAC,
∵l∥BC
∴直线l⊥平面PAC,
(II)如图建立坐标系得出:C(0,0,0),A(2,0,0),
E($\frac{1}{2}$,0,$\frac{\sqrt{3}}{2}$),F($\frac{1}{2}$,2,$\frac{\sqrt{3}}{2}$),P(1,0,$\sqrt{3}$),Q(2,y,0)
∴$\overrightarrow{CP}$=(1,0,$\sqrt{3}$)为平面AEF的法向量,$\overrightarrow{EF}$=(0,2,0),$\overrightarrow{PQ}$=(1,y,-$\sqrt{3}$)
∴cos<$\overrightarrow{CP}$,$\overrightarrow{PQ}$>=$\frac{-2}{2\sqrt{4+{y}^{2}}}$=$\frac{-1}{\sqrt{{y}^{2}+4}}$,cos<$\overrightarrow{PQ}$,$\overrightarrow{EF}$>=$\frac{2y}{2\sqrt{4+{y}^{2}}}$=$\frac{y}{\sqrt{4+{y}^{2}}}$,
设直线PQ分别与平面AEF、直线EF所成的角分别为α,β,α+β=$\frac{π}{2}$,
∴sinα=|$\frac{-1}{\sqrt{{y}^{2}+4}}$|,cosβ=|$\frac{y}{\sqrt{4+{y}^{2}}}$|,sinα=cosβ,
即1=|y|,求解y=±1,y=0,A(2,0,0),
存在Q(2,1,0)或Q(2,-1,0),
|AQ|=1.
点评 本题综合考查了空间直线,平面的位置关系,判断方法,空间向量解决存在性问题,运用代数方法求解几何问题,考查了学生的计算能力.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
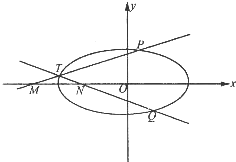 如图所示,椭圆C的离心率为$\frac{\sqrt{3}}{2}$,以坐标原点O为圆心,椭圆C的短半轴长为半径的圆与直线y=$\sqrt{3}$x+2相切.
如图所示,椭圆C的离心率为$\frac{\sqrt{3}}{2}$,以坐标原点O为圆心,椭圆C的短半轴长为半径的圆与直线y=$\sqrt{3}$x+2相切.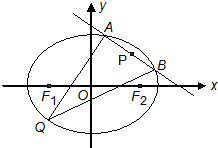 如图所示,已知椭圆C的方程为$\frac{x^2}{2}+{y^2}$=1,F1,F2分别是椭圆C的左、右焦点,直线AB:y=kx+m(k<0)与椭圆C交于不同的A,B两点.
如图所示,已知椭圆C的方程为$\frac{x^2}{2}+{y^2}$=1,F1,F2分别是椭圆C的左、右焦点,直线AB:y=kx+m(k<0)与椭圆C交于不同的A,B两点.