题目内容
11.侧棱和底面边长都是3$\sqrt{2}$的正四棱锥的外接球半径是36π.分析 正四棱锥外接球的球心在它的底面的中心,然后根据勾股定理解出球的半径,最后根据球的表面积公式求解即可.
解答 解:解:如图,侧棱和底面边长都是3$\sqrt{2}$的正四棱锥
设正四棱锥底面的中心为O,AB=BC=3$\sqrt{2}$
则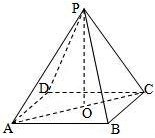 在直角三角形ABC中,AC=$\sqrt{2}$×AB=6,
在直角三角形ABC中,AC=$\sqrt{2}$×AB=6,
∴AO=CO=3,
在直角三角形PAO中,PO=$\sqrt{P{A}^{2}-A{O}^{2}}$=3,
∴正四棱锥的各个顶点到它的底面的中心的距离都为3,
∴正四棱锥外接球的球心在它的底面的中心,且球半径r=3,
球的表面积S=4πr2=36π,
故答案为:36π
点评 本题主要考查球的表面积,球的内接体问题,考查计算能力和空间想象能力,利用条件求出球的半径是解决本题的关键.

练习册系列答案
相关题目
19.已知命题p:?x∈R,ex>0命题q:?x∈R,x-2>x2,则( )
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∧(?q)是真命题 | D. | 命题p∨(?q)是假命题 |
6.双曲线$\frac{x^2}{10}-\frac{y^2}{2}$=1的焦距为( )
| A. | 2$\sqrt{3}$ | B. | 4$\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{3}$ |
5.复数z=$\frac{3+i}{1-i}$(i为虚数单位)在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
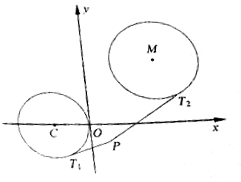 设圆C:(x+4)2+y2=16,动圆M:x2+y2-2ax-2(8-a)y+4a+22=0,平面内是还有存在定点P,过点P作圆C的一条切线,切点为T1,过点P作圆M的一条切线,切点为T2,使无穷多个圆M,满足$\frac{P{T}_{1}}{P{T}_{2}}$=$\frac{1}{2}$?如果存在,求出所有这样的点P;如果不存在,请说明理由.
设圆C:(x+4)2+y2=16,动圆M:x2+y2-2ax-2(8-a)y+4a+22=0,平面内是还有存在定点P,过点P作圆C的一条切线,切点为T1,过点P作圆M的一条切线,切点为T2,使无穷多个圆M,满足$\frac{P{T}_{1}}{P{T}_{2}}$=$\frac{1}{2}$?如果存在,求出所有这样的点P;如果不存在,请说明理由.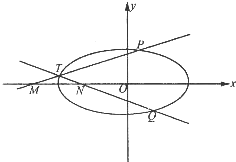 如图所示,椭圆C的离心率为$\frac{\sqrt{3}}{2}$,以坐标原点O为圆心,椭圆C的短半轴长为半径的圆与直线y=$\sqrt{3}$x+2相切.
如图所示,椭圆C的离心率为$\frac{\sqrt{3}}{2}$,以坐标原点O为圆心,椭圆C的短半轴长为半径的圆与直线y=$\sqrt{3}$x+2相切.