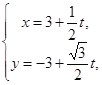题目内容
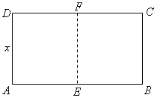
【题目】如图，点E为正方形ABCD边CD上异于点C，D的动点，将△ADE沿AE翻折成△SAE，使得平面SAE⊥平面ABCE，则下列三个说法中正确的个数是（ ）
①存在点E使得直线SA⊥平面SBC
②平面SBC内存在直线与SA平行
③平面ABCE内存在直线与平面SAE平行
A．0 B．1 C．2 D．3
【答案】B
【解析】
试题分析：对于命题①，若直线SA⊥平面SBC，则直线SA与平面SBC均垂直，则SA⊥BC，又由AD∥BC，则SA⊥AD，这与
为锐角矛盾，所以命题①不正确；对于命题②，因为平面
直线
，故平面
内的直线与
相交或异面，所以命题②不正确；对于命题③，取
的中点
，则CF∥AE，由线面平行的判定定理可得CF∥平面SAE，所以命题③正确，故应选
.
练习册系列答案
相关题目
【题目】在2016年6月英国“脱欧”公投前夕，为了统计该国公民是否有“留欧”意愿，该国某中学数学兴趣小组随机抽查了50名不同年龄层次的公民，调查统计他们是赞成“留欧”还是反对“留欧”．现已得知50人中赞成“留欧”的占60%，统计情况如下表：
年龄层次 | 赞成“留欧” | 反对“留欧” | 合计 |
18岁—19岁 | 6 | ||
50岁及50岁以上 | 10 | ||
合计 | 50 |
（1）请补充完整上述列联表；
（2）请问是否有97．5%的把握认为赞成“留欧”与年龄层次有关？请说明理由．
参考公式与数据：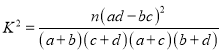
，其中
| 0．15 | 0．10 | 0．05 | 0．025 | 0．010 | 0．005 | 0．001 |
| 2．072 | 2．706 | 3．841 | 5．024 | 6．635 | 7．879 | 10．828 |
