题目内容
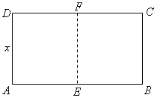
【题目】如图，某动物园要建造两间完全相同的矩形熊猫居室，其总面积为24平方米，设熊猫居室的一面墙
长为
米（2
）．
⑴用表示墙
的长；
⑵假设所建熊猫居室的墙壁造价（在墙壁高度一定的前提下）为每米1000元，请将墙壁的总造价
（元）表示为（米）的函数；
⑶当为何值时，墙壁的总造价最低？
【答案】（1） 
米；（2）
；（3）当x=4时，墙壁的总造价最低.
【解析】
试题分析：（1）根据面积
,可得结果；（2）总造价包含5面墙的造价，即
，
，相加就是总的造价；（3）根据（2）的结果，可根据基本不等式
求最值.
试题解析：（1）∵矩形熊猫居室的总面积=AB*AD=24平方米，设AD=x米
∴AB=
米（2≦x≦6）
（2）由题意得：墙壁的总造价函数y=
其中2≦x≦6，
（3）由y=
≧
=24000
当且仅当
，即x=4时取等号；
∴x=4时，y有最小值24000；所以，当x=4时，墙壁的总造价最低.
练习册系列答案
相关题目
