题目内容
【题目】已知函数![]() ,
,![]() ,
,![]() ,三个函数的定义域均为集合
,三个函数的定义域均为集合![]() .
.
(1)若![]() ,试判断集合
,试判断集合![]() 与
与![]() 的关系,并说明理由;
的关系,并说明理由;
(2)记![]() ,是否存在
,是否存在![]() ,使得对任意的实数
,使得对任意的实数![]() ,函数
,函数![]() 有且仅有两个零点?若存在,求出满足条件的最小正整数
有且仅有两个零点?若存在,求出满足条件的最小正整数![]() ;若不存在,说明理由.(以下数据供参考:
;若不存在,说明理由.(以下数据供参考:![]() ,
,![]() )
)
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)![]() ,利用导数工具得
,利用导数工具得![]()
![]()
![]()
![]()
![]() ;(2)令
;(2)令![]() ,
,![]() .利用导数工具和零点存在性定理可知:
.利用导数工具和零点存在性定理可知: ![]() ,
,![]() ,由于
,由于![]() ,
,![]() ,
,![]() ,
,![]() ,由零点存在性定理可知:
,由零点存在性定理可知:![]() ,函数
,函数![]() 在定义域内有且仅有一个零点.
在定义域内有且仅有一个零点.![]() ,函数
,函数![]() 在定义域内有且仅有一个零点.假设存在
在定义域内有且仅有一个零点.假设存在![]() 使得
使得![]() ,
,

![]()
![]() ,令
,令![]() ,利用导数工具可得
,利用导数工具可得![]() .
.
试题解析:(1)![]() ,
,![]() .
.
易知![]() 在
在![]() 上递减,∴
上递减,∴![]() .
.
存在![]() ,使得
,使得![]() ,函数
,函数![]() 在
在![]() 递增,在
递增,在![]() 递减,
递减,![]() .
.
由![]() 得
得![]() ,
,
![]() ,
,
∴![]() ,
,![]() .
.
(2)令![]() ,
,![]() .
.
①![]() ,
,![]() ,由于
,由于![]() ,
,![]() ,
,![]() ,
,![]() ,由零点存在性定理可知:
,由零点存在性定理可知:
![]() ,函数
,函数![]() 在定义域内有且仅有一个零点.
在定义域内有且仅有一个零点.
②![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
同理可知:
![]() ,函数
,函数![]() 在定义域内有且仅有一个零点.
在定义域内有且仅有一个零点.
③假设存在![]() 使得
使得![]() ,
,
 消
消![]() 得
得![]() ,
,
令![]() ,
,![]() ,
,
∴![]() 递增.∵
递增.∵![]() ,
,![]() ,
,
∴![]() ,
,
此时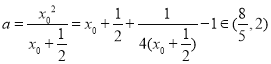 ,
,
所以满足条件的最小整数![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目