题目内容
【题目】如图,在平面直角坐标系xOy中,椭圆C:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,短轴长是2.
,短轴长是2.
(1)求椭圆C的方程;
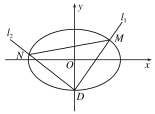
(2)设椭圆C的下顶点为D,过点D作两条互相垂直的直线l1,l2,这两条直线与椭圆C的另一个交点分别为M,N.设l1的斜率为k(k≠0),△DMN的面积为S,当![]() ,求k的取值范围.
,求k的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由e=![]() ,2b=2,a2=b2+c2构造方程组,解出a,b即可得椭圆方程;(2)设l1的方程为y=kx-1代入椭圆方程,求出M的坐标,可得|DM|,用
,2b=2,a2=b2+c2构造方程组,解出a,b即可得椭圆方程;(2)设l1的方程为y=kx-1代入椭圆方程,求出M的坐标,可得|DM|,用![]() 代替k,可得|DN|,求出△DMN的面积S,可得
代替k,可得|DN|,求出△DMN的面积S,可得![]() ,解不等式
,解不等式![]() >
>![]() 可得k的取值范围.
可得k的取值范围.
(1)设椭圆C的半焦距为c,则由题意得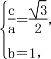 又a2=b2+c2,解得a=2,b=1,
又a2=b2+c2,解得a=2,b=1,
∴椭圆方程为![]() +y2=1.
+y2=1.
(2)由(1)知,椭圆C的方程为![]() +y2=1,
+y2=1,
所以椭圆C与y轴负半轴交点为D(0,-1).
因为l1的斜率存在,所以设l1的方程为y=kx-1.
代入![]() +y2=1,得M
+y2=1,得M![]() ,
,
从而|DM|=![]() =
=![]() .
.
用-![]() 代替k得|DN|=
代替k得|DN|=![]() .
.
所以△DMN的面积S=![]() ·
·![]() ×
×![]() =
=![]() .
.
则![]() =
=![]() ,
,
因为![]() >
>![]() ,即
,即![]() >
>![]() ,
,
整理得4k4-k2-14<0,解得-![]() <k2<2,
<k2<2,
所以0<k2<2,即-![]() <k<0或0<k<
<k<0或0<k<![]() .
.
从而k的取值范围为(-![]() ,0)∪(0,
,0)∪(0,![]() ).
).

练习册系列答案
相关题目
【题目】某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据.
x | 6 | 8 | 10 | 12 |
y | 2 | 3 | 5 | 6 |
(1)请根据上表提供的数据,求出y关于x的线性回归方程![]() ;
;
(2)判断该高三学生的记忆力x和判断力是正相关还是负相关;并预测判断力为4的同学的记忆力.
(参考公式: )
)