题目内容
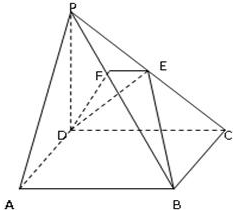 在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ACD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ACD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.(1)求证:PA∥平面EDB;
(2)求证:PF=
| 1 |
| 3 |
(3)求二面角C-PB-D的大小.
考点:二面角的平面角及求法,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)连结AC,BD,交于点O,连结OE,由已知得OE∥AP,由此能证明PA∥平面EDB.
(2)以D为原点,DA为x轴,DC为y轴,DP为z轴,建立空间直角坐标系,利用向量法能证明PF=
PB.
(3)求出平面DBP的法向量和平面PBC的法向量,利用向量法能求出二面角C-PB-D的大小.
(2)以D为原点,DA为x轴,DC为y轴,DP为z轴,建立空间直角坐标系,利用向量法能证明PF=
| 1 |
| 3 |
(3)求出平面DBP的法向量和平面PBC的法向量,利用向量法能求出二面角C-PB-D的大小.
解答:
(1)证明: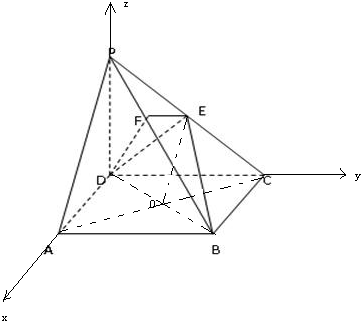 连结AC,BD,交于点O,
连结AC,BD,交于点O,
∵底面ABCD是正方形,∴O是AC中点,
连结OE,∵E是PC中点,
∴OE∥AP,
∵AP不包含于平面EDB,OE?平面EDB,
∴PA∥平面EDB.
(2)证明:以D为原点,DA为x轴,
DC为y轴,DP为z轴,
建立空间直角坐标系,
设PD=DC=2,
则P(0,0,2),B(2,2,0),
C(0,2,0),E(0,1,1),
=(2,2,-2),
设F(a,b,c),
=λ
,
则(a,b,c-2)=(2λ,2λ,-2λ),
∴F(2λ,2λ,2-2λ),
=(2λ,2λ-1,1-2λ),
∵EF⊥PB交PB于点F,
∴
•
=4λ+4λ-2-2+4λ=0,
解得λ=
,
∴PF=
PB.
(3)解:
=(0,0,2),
=(2,2,0),
设平面DBP的法向量
=(x,y,z),
则
,取x=1,得
=(1,-1,0).
=(2,2,-2),
=(0,2,-2),
设平面PBC的法向量
=(a,b,c),
则
,取b=1,得
=(0,1,1),
∴cos<
,
>=
=-
,
∴二面角C-PB-D的大小为60°.
 连结AC,BD,交于点O,
连结AC,BD,交于点O,∵底面ABCD是正方形,∴O是AC中点,
连结OE,∵E是PC中点,
∴OE∥AP,
∵AP不包含于平面EDB,OE?平面EDB,
∴PA∥平面EDB.
(2)证明:以D为原点,DA为x轴,
DC为y轴,DP为z轴,
建立空间直角坐标系,
设PD=DC=2,
则P(0,0,2),B(2,2,0),
C(0,2,0),E(0,1,1),
| PB |
设F(a,b,c),
| PF |
| PB |
则(a,b,c-2)=(2λ,2λ,-2λ),
∴F(2λ,2λ,2-2λ),
| EF |
∵EF⊥PB交PB于点F,
∴
| EF |
| PB |
解得λ=
| 1 |
| 3 |
∴PF=
| 1 |
| 3 |
(3)解:
| DP |
| DB |
设平面DBP的法向量
| n |
则
|
| n |
| PB |
| PC |
设平面PBC的法向量
| m |
则
|
| m |
∴cos<
| n |
| m |
| -1 | ||||
|
| 1 |
| 2 |
∴二面角C-PB-D的大小为60°.
点评:本题考查PA∥平面EDB的证明,考查PF=
PB的证明,考查二面角C-PB-D的大小的求法,解题时要注意向量法的合理运用.
| 1 |
| 3 |

练习册系列答案
相关题目
 抛物线有光学性质,从焦点出发的光经抛物线反射后沿平行于抛物线的对称轴方向射出,今有抛物线y2=2px(p>0),一光源在点A(6,4)处,由其发出的光线沿平行于抛物线的对称轴的方向射向抛物线上的B点,反射后,又射向抛物线上的C点,再反射后沿平行于抛物线的对称轴的方向射出,途中遇到直线l:x-y-7=0上的点D,再反射后又射回到A点,如图所示,则此抛物线的方程为( )
抛物线有光学性质,从焦点出发的光经抛物线反射后沿平行于抛物线的对称轴方向射出,今有抛物线y2=2px(p>0),一光源在点A(6,4)处,由其发出的光线沿平行于抛物线的对称轴的方向射向抛物线上的B点,反射后,又射向抛物线上的C点,再反射后沿平行于抛物线的对称轴的方向射出,途中遇到直线l:x-y-7=0上的点D,再反射后又射回到A点,如图所示,则此抛物线的方程为( )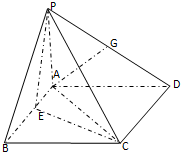 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,A点在PD上的射影为G点,E点在AB上,平面PEC⊥平面PDC.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,A点在PD上的射影为G点,E点在AB上,平面PEC⊥平面PDC.