题目内容
7.以下五个命题:①“事件A,B是互斥事件”是“事件A,B是对立事件”的充分不必要条件;
②设y=f(x)是R上的任意函数,则函数h(x)=f(x)-f(-x)是偶函数;
③函数f(x)=2x+x3-2在区间(0,1)内有一个零点;
④若$\frac{1}{x}$+$\frac{9}{y}$=1(x,y∈R+),则x+y的最小值为12;
⑤若干个能唯一确定一个数列的量称为该数列的“基量”;若{an}是公比为q的无穷等比数列,则“S1与S2”与“q与an”(其中n为大于1的整数,Sn为{an}的前n项和)均为数列{an}的“基量”.
其中的真命题对应的序号为③⑤.
分析 ①注意互斥事件不一定对立,对立事件一定是互斥事件.
②由于函数的定义域都是R,故只看f(-x)与f(x)的关系,再根据奇函数、偶函数的定义作出判断.
③根据函数f(x)=2x+x3-2在区间(0,1)内单调递增,f(0)f(1)<0,可得函数在区间(0,1)内有唯一的零点.
④利用基本不等式的性质即可得出.
⑤由通项公式,数列{an} 能够确定,从而可判断.
解答 解:①,由“A,B是互斥事件”不一定有“A,B是对立事件”,
反之,由“A,B是对立事件”一定有“A,B是互斥事件”,
所以命题“A,B是互斥事件”是命题“A,B是对立事件”的必要不充分条件,所以命题①不正确;
②,h(x)=f(x)-f(-x),h(-x)=f(-x)-f(x)=-h(x),故为奇函数,故②不正确.
③,由于函数f(x)=2x+x3-2在区间(0,1)内单调递增,
又f(0)=-1<0,f(1)=1>0,所以f(0)f(1)<0,
故函数f(x)=2x+x3-2在区间(0,1)内有唯一的零点,故③正确.
④∵x,y∈R+,$\frac{1}{x}$+$\frac{9}{y}$=1,x+y=(x+y)($\frac{1}{x}$+$\frac{9}{y}$)=10+$\frac{y}{x}$$+\frac{9x}{y}$≥10+$2\sqrt{\frac{y}{x}×\frac{9x}{y}}$=10+6=16,
当且仅当x=4,y=12时,取等号.∴x+y的最小值为16.故④不正确.
⑤:对“S1和S2”,可知a1和a2.由 $\frac{{a}_{2}}{{a}_{1}}$可得公比q,故能确定是该数列的“基量”;
对“q与an”,由{an}是等比数列得an=a1qn-1,故数列{an} 能够确定是数列{an} 的一个“基量”;故⑤正确.
故答案为:③⑤
点评 本题考查了命题的真假的判断,考查了全称命题的否定的格式,考查了充要条件判断的方法,函数的奇偶性的判断方法,函数零点的定义以及函数零点判定定理的应用,是中档题型.

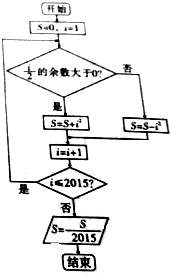
| A. | 1006 | B. | 1008 | C. | 2015 | D. | 2016 |
| A. | $\frac{{\sqrt{5}}}{4}$ | B. | $\frac{{\sqrt{6}}}{6}$ | C. | $\frac{{\sqrt{5}}}{6}$ | D. | 2 |
| 做不到“光盘” | 能做到“光盘” | |
| 男 | 45 | 10 |
| 女 | 30 | 15 |
| P(K2≥k) | 0.10 | 0.05 | 0.01 |
| k | 2.706 | 3.841 | 6.635 |
| A. | 在犯错误的概率不超过1%的前提下,认为“该校学生能否做到‘光盘’与性别无关” | |
| B. | 有99%以上的把握认为“该校学生能否做到‘光盘’与性别有关” | |
| C. | 在犯错误的概率不超过10%的前提下,认为“该校学生能否做到‘光盘’与性别有关” | |
| D. | 有90%以上的把握认为“该校学生能否做到‘光盘’与性别无关” |
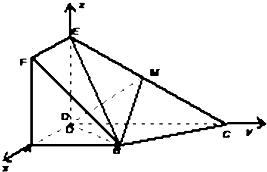 如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=$\frac{1}{2}$CD=2,当点M为EC中点时.
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=$\frac{1}{2}$CD=2,当点M为EC中点时.