题目内容

12．已知（x-1）n的二项展开式的奇数项二项式系数和为64，若（x-1）n=a0+a1（x+1）+a2（x+1）2+…+an（x+1）n，则a1等于448．

分析 由条件求得n=7，可得[-2+（x+1）]7=a0+a1（x+1）+a2（x+1）2+…+a7（x+1）7，再利用通项公式求得a1 的值．

解答 解：由题意可得2n=2×64，∴n=7，故（x-1）7=[-2+（x+1）]7
=a0+a1（x+1）+a2（x+1）2+…+a7（x+1）7，
故a1=${C}_{7}^{1}$•（-2）6 7×64=448，
故答案为：448．

点评 本题主要考查二项式定理的应用，二项式展开式的通项公式，属于基础题．

练习册系列答案
相关题目
2．已知数列{an}、{bn}中，对任何正整数n都有：a1bn+a2bn-1+a3bn-2…+an-1b2+anb1=2n+1-n-2．
（1）若数列{an}是首项和公差都是1的等差数列，求b1，b2，并证明数列{bn}是等比数列；
（2）若数列{bn}是等比数列，数列{an}是否是等差数列，若是请求出通项公式，若不是请说明理由；
（3）若数列{an}是等差数列，数列{bn}是等比数列，求证：$\frac{1}{{a}_{1}{b}_{1}}$+$\frac{1}{{a}_{2}{b}_{2}}$+…+$\frac{1}{{a}_{n}{b}_{n}}$＜$\frac{3}{2}$．
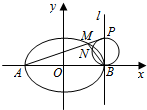3．已知A、B分别为曲线C：$\frac{{x}^{2}}{{a}^{2}}$+y2=1（a＞0）与x轴的左、右两个交点，直线l过点B且与x轴垂直，P为l上异于点B的点，连结AP与曲线C交于点M．
（1）若曲线C为圆，且|BP|=$\frac{2\sqrt{3}}{3}$，求弦AM的长；
（2）设N是以BP为直径的圆与线段BM的交点，若O、N、P三点共线，求曲线C的方程．
20．已知数列{an}的首项a1=1，an+1=$\frac{3{a}_{n}}{{a}_{n}+1}$，n∈N+．
（Ⅰ）证明：数列{$\frac{1}{{a}_{n}}-\frac{1}{2}$}是等比数列；
（Ⅱ）求数列{$\frac{2n}{{a}_{n}}$}的前n项和Sn．
7．以下五个命题：
①“事件A，B是互斥事件”是“事件A，B是对立事件”的充分不必要条件；
②设y=f（x）是R上的任意函数，则函数h（x）=f（x）-f（-x）是偶函数；
③函数f（x）=2x+x3-2在区间（0，1）内有一个零点；
④若$\frac{1}{x}$+$\frac{9}{y}$=1（x，y∈R+），则x+y的最小值为12；
⑤若干个能唯一确定一个数列的量称为该数列的“基量”；若{an}是公比为q的无穷等比数列，则“S1与S2”与“q与an”（其中n为大于1的整数，Sn为{an}的前n项和）均为数列{an}的“基量”．
其中的真命题对应的序号为③⑤．
17．已知函数f（x）=sin2x-cos2x，则f（x）在$x∈[{0，\frac{π}{2}}]$时的值域是[-1，$\sqrt{2}$]；若将函数y=f（x）的图象向左平移a（a＞0）个单位长度得到的图象恰好关于直线$x=\frac{π}{4}$对称，则实数a的最小值为$\frac{π}{8}$．
4．△ABC外接圆的半径为1，圆心为O，且$\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AO}，|\overrightarrow{AB}|=\sqrt{3}|\overrightarrow{OA}|，则\overrightarrow{CA}•\overrightarrow{CB}$的值是1．
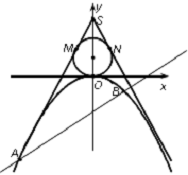1．如图所示，已知点S（0，3），过点S作直线SM，SN与圆Q：x2+y2-2y=0和抛物线C：x2=-2py（p＞0）都相切．
（1）求抛物线C和两切线的方程；
（2）设抛物线的焦点为F，过点P（0，-2）的直线与抛物线相交于A，B两点，与抛物线的准线交于点C（其中点B靠近点C），且|AF|=5，求△BCF与△ACF的面积之比．
2．已知向量$\overrightarrow{a}$=（-2，4），$\overrightarrow{b}$=（5，2），则向量$\overrightarrow{a}$+$\overrightarrow{b}$=（3，6）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网