题目内容
2.某校通过随机询问100名性别不同的学生是否能做到“光盘”行动,得到所示联表:| 做不到“光盘” | 能做到“光盘” | |
| 男 | 45 | 10 |
| 女 | 30 | 15 |
| P(K2≥k) | 0.10 | 0.05 | 0.01 |
| k | 2.706 | 3.841 | 6.635 |
| A. | 在犯错误的概率不超过1%的前提下,认为“该校学生能否做到‘光盘’与性别无关” | |
| B. | 有99%以上的把握认为“该校学生能否做到‘光盘’与性别有关” | |
| C. | 在犯错误的概率不超过10%的前提下,认为“该校学生能否做到‘光盘’与性别有关” | |
| D. | 有90%以上的把握认为“该校学生能否做到‘光盘’与性别无关” |
分析 通过图表读取数据,代入观测值公式计算,然后参照临界值表即可得到正确结论
解答 解:由2×2列联表得到a=45,b=10,c=30,d=15.
则a+b=55,c+d=45,a+c=75,b+d=25,ad=675,bc=300,n=100.
代入K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c))(b+d)}$,
得k2的观测值k=$\frac{100(675-300)^{2}}{55×45×75×25}$.
因为2.706<3.030<3.841.
所以有90%以上的把握认为“该市居民能否做到‘光盘’与性别有关”.
即在犯错误的概率不超过10%的前提下,认为“该校学生能否做到‘光盘’与性别有关”
故选C.
点评 本题是一个独立性检验,我们可以利用临界值的大小来决定是否拒绝原来的统计假设,若值较大就拒绝假设,即拒绝两个事件无关,此题是基础题.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
12.某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在(29.94,30.06)的零件为优质品.从两个分厂生产的零件中个抽出500 件,量其内径尺寸的结果如下表(表1为甲厂,表2为乙 厂):
表1
表2
(1)试分别估计两个分厂生产的零件的优质品率;
(2)由于以上统计数据填下面2×2列联表(填写在答题卡的2×2列联表中),并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”.
表1
| 分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
| 频数 | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
| 分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
| 频数 | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
(2)由于以上统计数据填下面2×2列联表(填写在答题卡的2×2列联表中),并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”.
13.函数y=x4(2-x2)(0<x<$\sqrt{2}$)的最大值是( )
| A. | 0 | B. | 1 | C. | $\frac{16}{27}$ | D. | $\frac{32}{27}$ |
14.已知α,β∈($\frac{3π}{2}$,2π),满足tan(α+β)-2tanβ=0,则tanα的最小值是( )
| A. | $\frac{{3\sqrt{2}}}{4}$ | B. | -$\frac{{\sqrt{2}}}{4}$ | C. | -$\frac{{3\sqrt{2}}}{4}$ | D. | $\frac{{\sqrt{2}}}{4}$ |
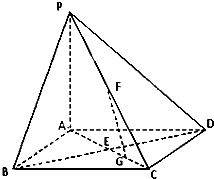 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.