题目内容
17.在△ABC中,已知a,b,c为三角形的三边,a=2,b=2$\sqrt{2}$,C=15°,解此三角形(用余弦定理解答)分析 由C的度数求出sinC与cosC的值,再由a与b的值,利用余弦定理求出c的值,根据正弦定理求出sinA与sinB的值,进而确定出A与B的度数.
解答 解:∵C=15°,
∴cosC=cos(45°-30°)=cos45°cos30°+sin45°sin30°=$\frac{\sqrt{2}}{2}$×$\frac{\sqrt{3}}{2}$+$\frac{\sqrt{2}}{2}$×$\frac{1}{2}$=$\frac{\sqrt{6}+\sqrt{2}}{4}$,
sinC=sin(45°-30°)=sin45°cos30°-cos45°sin30°=$\frac{\sqrt{6}-\sqrt{2}}{4}$,
∵a=2,b=2$\sqrt{2}$,
∴由余弦定理得:c2=a2+b2-2abcosC=4+8-8$\sqrt{2}$×$\frac{\sqrt{6}+\sqrt{2}}{4}$=8-4$\sqrt{3}$=2($\sqrt{3}$-1)2,
解得:c=$\sqrt{2}$($\sqrt{3}$-1)=$\sqrt{6}$-$\sqrt{2}$,
由正弦定理$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$得:$\frac{2}{sinA}$=$\frac{2\sqrt{2}}{sinB}$=$\frac{\sqrt{6}-\sqrt{2}}{\frac{\sqrt{6}-\sqrt{2}}{4}}$=4,
∴sinA=$\frac{1}{2}$,sinB=$\frac{\sqrt{2}}{2}$,
∵a<b,∴A<B,
∴A=30°,B=135°.
点评 此题考查了正弦、余弦定理,以及两角和与差的正弦、余弦函数公式,熟练掌握定理及公式是解本题的关键.

| A. | 400 | B. | 500 | C. | 600 | D. | 800 |
| A. | $-\frac{1}{2}{a^2}$ | B. | $-\frac{{\sqrt{3}}}{2}{a^2}$ | C. | $\frac{1}{2}{a^2}$ | D. | $\frac{{\sqrt{3}}}{2}{a^2}$ |
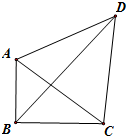 如图,在四边形ABCD中,AB⊥BC,AB=3,BC=4,△ACD是等边三角形,则$\overrightarrow{AC}•\overrightarrow{BD}$的值为$\frac{7}{2}$.
如图,在四边形ABCD中,AB⊥BC,AB=3,BC=4,△ACD是等边三角形,则$\overrightarrow{AC}•\overrightarrow{BD}$的值为$\frac{7}{2}$.