Question

【题目】已知圆的圆心在抛物线上，圆过原点且与抛物线的准线相切.

（1）求该抛物线的方程；

（2）过抛物线焦点的直线交抛物线于， 两点，分别在点， 处作抛物线的两条切线交于点，求三角形面积的最小值及此时直线的方程.

Answer 1

【答案】(1) ;(2) 三角形PAB面积最小值为4，此时直线L的方程为.

【解析】【试题分析】(1)写出圆心/半径,焦点坐标和准线方程,根据原点在圆上及圆心到抛物线的距离建立方程,解方程组求得的值,由此得到抛物线方程.(2)设出直线的方程,联立直线的方程和抛物线线的方程,写出韦达定理,利用导数求出切线的方程,求出交点的坐标,利用弦长公式和点到直线距离公式写出三角形面积的表达式,并由此求得最小值.

【试题解析】

（1）由已知可得圆心，半径，焦点，准线

因为圆C与抛物线F的准线相切，所以，

且圆C过焦点F，

又因为圆C过原点，所以圆心C必在线段OF的垂直平分线上，

即

所以，即，抛物线F的方程为

（2）易得焦点，直线L的斜率必存在，设为k，即直线方程为

设

得，，

对求导得，即

直线AP的方程为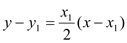，即，

同理直线BP方程为

设，

联立AP与BP直线方程解得，即

所以，点P到直线AB的距离

所以三角形PAB面积，当仅当时取等号

综上：三角形PAB面积最小值为4，此时直线L的方程为.