题目内容
12.已知抛物线y2=8x的焦点为F,点P(x,y)为该抛物线上的动点,若点A(-2,0),则$\frac{|PA|}{|PF|}$的最大值是$\sqrt{2}$.分析 过P作抛物线准线的垂线,垂足为M,则|PF|=|PM|,可得$\frac{|PA|}{|PF|}$=$\frac{1}{sin∠MAP}$,求出过A抛物线的切线方程,即可得出结论.
解答 解:过P作抛物线准线的垂线,垂足为M,则|PF|=|PM|,
∵抛物线y2=8x的焦点为F(-2,0),点A(-2,0)
∴$\frac{|PA|}{|PF|}$=$\frac{1}{sin∠MAP}$,
设过A抛物线的切线方程为y=k(x+2),代入抛物线方程可得k2x2+(4k2-8)x+4k2=0,
∴△=(4k2-8))2-16k4=0,
∴k=±1
∴$\frac{1}{sin∠MAP}$∈[1,$\sqrt{2}$].
故答案为:$\sqrt{2}$.
点评 本题考查抛物线的简单性质,考查直线与抛物线的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
20.已知在△ABC中,a=$\sqrt{5},b=\sqrt{15},A={30°}$,则c等于( )
| A. | 2$\sqrt{5}$ | B. | $\sqrt{5}$或2$\sqrt{5}$ | C. | $\sqrt{15}$ | D. | 以上都不对 |
2.已知对于任意实数a(a>0,且a≠1),函数f(x)=7+ax-1的图象恒过点P,则P点的坐标是( )
| A. | (1,8) | B. | (1,7) | C. | (0,8) | D. | (8,0) |
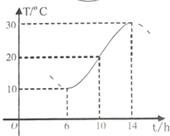 如图,某地一天从6-14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(A>0,ω>0,0<φ<π),则该函数的表达式为y=10sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20,x∈[6,14].
如图,某地一天从6-14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(A>0,ω>0,0<φ<π),则该函数的表达式为y=10sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20,x∈[6,14].