题目内容
6.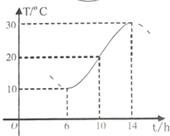 如图,某地一天从6-14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(A>0,ω>0,0<φ<π),则该函数的表达式为y=10sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20,x∈[6,14].
如图,某地一天从6-14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(A>0,ω>0,0<φ<π),则该函数的表达式为y=10sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20,x∈[6,14].
分析 通过函数的图象,求出A,b,求出函数的周期,推出ω,利用函数经过(10,20)求出φ,得到函数的解析式.
解答 解:由题意以及函数的图象可知,A=10,b=20,T=2(14-6)=16,所以ω=$\frac{2π}{T}$=$\frac{π}{8}$,
函数经过(10,20)所以20=10sin($\frac{π}{8}$×10+φ)+20,又0<φ<π,所以φ=$\frac{3π}{4}$,
所以函数的解析式:y=10sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20,x∈[6,14].
故答案为:y=10sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20,x∈[6,14].
点评 通过函数的图象求出函数的解析式,是三角函数常考题型,注意图象经过的特殊点,注意函数解析式的范围容易出错遗漏.

练习册系列答案
相关题目
16.已知D为△ABC的边BC上的中点,△ABC所在平面内有一点P,满足$\overrightarrow{PA}$+$\overrightarrow{BP}$+$\overrightarrow{CP}$=0,则$\frac{|\overrightarrow{PD}|}{|\overrightarrow{AD}|}$等于( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
14.若直线y=k(x+1)与圆x2+y2=1相交于A,B两点,且$\overrightarrow{OA}$$•\overrightarrow{OB}$=-$\frac{1}{2}$,则实数k的值为( )
| A. | $±\frac{\sqrt{3}}{3}$ | B. | $±\frac{\sqrt{3}}{2}$ | C. | ±1 | D. | $±\sqrt{3}$ |
1.为规范办学,市教育局督导组对某所高中进行了抽样调查,抽到的班级一共有52名学生,现将该班学生随机编号,用系统抽样的方法抽到一个容量为4的样本,已知7号,33号,46号同学在样本中,那么样本中另一位同学的编号应该是( )
| A. | 13 | B. | 19 | C. | 20 | D. | 51 |
11.甲、乙两人独立地解决同一个问题,甲能解决这个问题的概率是P1,乙能解决这个问题的概率是P2,那么至少有一人能解决这个问题的概率是( )
| A. | P1+P2 | B. | P1P2 | C. | 1-P1P2 | D. | 1-(1-P1)(1-P2) |
18.曲线y=x3-2x+4在点(1,3)处的切线方程为( )
| A. | y=x+2 | B. | y=-x+1 | C. | y=x-2 | D. | y=-x+4 |