题目内容
4．满足方程x2-2x+3+（9y2-6y+1）i=0的实数对（x，y）表示的点的个数为0．分析 根据条件和复数相等的定义列出方程组，求出方程组的解即可．
解答 解：∵x2-2x+3+（9y2-6y+1）i=0，
∴$\left\{\begin{array}{l}{{x}^{2}-2x+3=0}\\{9{y}^{2}-6y+1=0}\end{array}\right.$，又x2-2x+3=（x-1）2+2＞0，
则此方程组无解，
所以满足条件的实数对（x，y）为0个，
故答案为：0．
点评 本题考查复数相等的定义，以及方程思想，属于基础题．
练习册系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
相关题目
18．曲线y=x3-2x+4在点（1，3）处的切线方程为（ ）
| A． | y=x+2 | B． | y=-x+1 | C． | y=x-2 | D． | y=-x+4 |
15．如果方程$\frac{x^2}{m+2}+\frac{y^2}{m+1}=1$表示双曲线，则实数m的取值范围是（ ）
| A． | （-2，-1） | B． | （-∞，-2）∪（-1，+∞） | C． | （-1，-1） | D． | （-3，-2） |
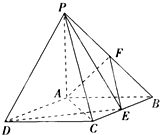如图所示，四棱锥P-ABCD中，底面ABCD是矩形，PA⊥底面ABCD，PA=AB=1，AD=$\sqrt{3}$，点F是PB的中点，点E在棱BC上移动．