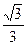题目内容
已知点F1、F2分别是椭圆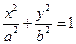
的左、右焦点，过F1且垂直于x轴的直线与椭圆交于A、B两点，若△ABF2为正三角形，则该椭圆的离心率
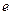是_____________.
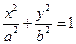的左、右焦点，过F1且垂直于x轴的直线与椭圆交于A、B两点，若△ABF2为正三角形，则该椭圆的离心率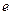是_____________.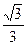 
略
练习册系列答案
导学全程练创优训练系列答案
相关题目
导学全程练创优训练系列答案题目内容
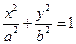的左、右焦点，过F1且垂直于x轴的直线与椭圆交于A、B两点，若△ABF2为正三角形，则该椭圆的离心率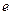是_____________. 导学全程练创优训练系列答案
轴上，离心率为
，两条准线间的距离为6. 椭圆W的左焦点为
，过左准线与
任作一条斜率不为零的直线
与椭圆W交于不同的两点
、
，点
.
(
)；
中，椭圆
的焦距为2c，以O为圆心，
为半径作圆
，若过
作圆
：
的右顶点为
，过
在抛物线
：
上，
．线段
的中点与
的中点的横坐标相等时，求
的最小值．
过点
，且长轴长等于4．
是椭圆C的两个焦点，⊙O是以F1F2为直径的圆，直线l: y=kx+m与⊙O相切，并与椭圆C交于不同的两点A、B，若
，求
的值
，则以
为焦点，且过
两点的椭圆的离心率为______．
（
为参数），则它的离心率为 ． 
，
分别为椭圆
的左右焦点，过
与椭圆
相交于
,
两点，直线
，
。
,求椭圆