题目内容
如图一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2。将△ABD沿边AB折起, 使得△ABD与△ABC成30o的二面角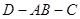 ,如图二,在二面角
,如图二,在二面角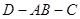 中.
中.

(1) 求D、C之间的距离;
(2) 求CD与面ABC所成的角的大小;
(3) 求证:对于AD上任意点H,CH不与面ABD垂直。
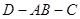 ,如图二,在二面角
,如图二,在二面角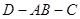 中.
中.
(1) 求D、C之间的距离;
(2) 求CD与面ABC所成的角的大小;
(3) 求证:对于AD上任意点H,CH不与面ABD垂直。
(1)|CD|= =
= ;
;
(2) =
= ; (3) CH不与面ABD垂直。
; (3) CH不与面ABD垂直。
 =
= ;
; (2)
 =
= ; (3) CH不与面ABD垂直。
; (3) CH不与面ABD垂直。试题分析:依题意,
 ABD=90o,建立如图的坐标系使得△ABC在yoz平面上,
ABD=90o,建立如图的坐标系使得△ABC在yoz平面上, △ABD与△ABC成30o的二面角,
△ABD与△ABC成30o的二面角, 
 DBY=30o,又AB=BD=2,
DBY=30o,又AB=BD=2,  A(0,0,2),B(0,0,0),
A(0,0,2),B(0,0,0),C(0,
 ,1),D(1,
,1),D(1, ,0),
,0), (1)|CD|=
(1)|CD|= =
= ……… 5分
……… 5分(2)
 x轴与面ABC垂直,故(1,0,0)是面ABC的一个法向量。
x轴与面ABC垂直,故(1,0,0)是面ABC的一个法向量。设CD与面ABC成的角为
 ,而
,而 = (1,0,-1),
= (1,0,-1), sin
sin =
= =
=


 [0,
[0, ],
],
 =
= ; 8分
; 8分(3) 设
 =t
=t = t(1,
= t(1, ,-2)= (t,
,-2)= (t, t,-2 t),
t,-2 t), =
= +
+ =(0,-
=(0,- ,1) +(t,
,1) +(t, t,-2 t) = (t,
t,-2 t) = (t, t-
t- ,-2 t+1),
,-2 t+1),若


 ,则 (t,
,则 (t, t-
t- ,-2 t+1)·(0,0,2)="0" 得t=
,-2 t+1)·(0,0,2)="0" 得t= , 10分
, 10分此时
 =(
=( ,-
,- ,0),
,0),而
 =(1,
=(1, ,0),
,0), ·
· =
= -
- =-1
=-1 0,
0,
 和
和 不垂直,
不垂直,即CH不可能同时垂直BD和BA,即CH不与面ABD垂直。 12分
点评:典型题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤,利用向量则能简化证明过程。本题利用空间向量,简化了证明过程,但对计算能力要求较高。

练习册系列答案
相关题目
 的棱线长为1,线段
的棱线长为1,线段 上有两个动点E,F,且
上有两个动点E,F,且 ,则三棱锥
,则三棱锥 的体积为
的体积为  α,则b∥α
α,则b∥α 是平面
是平面 内的一条定直线,
内的一条定直线, 是平面
是平面 经过点
经过点 角,则直线
角,则直线 的轨迹是
的轨迹是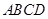 与正三角形
与正三角形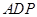 所在的平面相互垂直,且
所在的平面相互垂直,且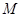 、
、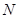
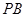 、
、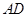 中点.
中点.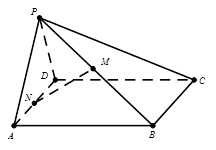
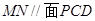 ;
;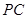 与平面
与平面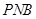 所成角的正弦值.
所成角的正弦值.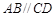 ,
,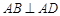 ,且
,且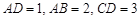 ,E、F分别为线段CD、AB上的点,且
,E、F分别为线段CD、AB上的点,且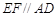 .将梯形沿EF折起,使得平面
.将梯形沿EF折起,使得平面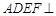 平面BCEF,折后BD与平面ADEF所成角正切值为
平面BCEF,折后BD与平面ADEF所成角正切值为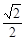 .
.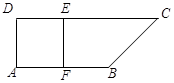
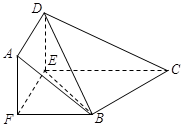
 平面BDE;
平面BDE; 中,
中,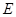 ,
,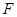 分别是棱
分别是棱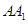 ,
,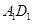 的中点,则
的中点,则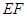 与平面
与平面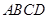 所成的角的大小是 .
所成的角的大小是 .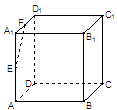
 N
N 个平面,任意三个平面不经过同一条直线.若这
个平面,任意三个平面不经过同一条直线.若这 个平面将空间分成
个平面将空间分成 个部分,则
个部分,则 ,
, .
.