题目内容
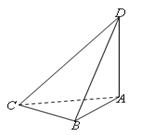
如图,在直角梯形ABCD中,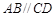 ,
,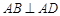 ,且
,且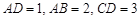 ,E、F分别为线段CD、AB上的点,且
,E、F分别为线段CD、AB上的点,且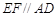 .将梯形沿EF折起,使得平面
.将梯形沿EF折起,使得平面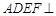 平面BCEF,折后BD与平面ADEF所成角正切值为
平面BCEF,折后BD与平面ADEF所成角正切值为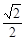 .
.
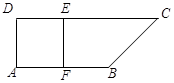
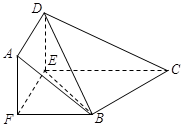
(Ⅰ)求证: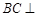 平面BDE;
平面BDE;
(Ⅱ)求平面BCEF与平面ABD所成二面角(锐角)的大小.
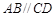 ,
,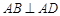 ,且
,且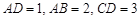 ,E、F分别为线段CD、AB上的点,且
,E、F分别为线段CD、AB上的点,且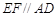 .将梯形沿EF折起,使得平面
.将梯形沿EF折起,使得平面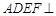 平面BCEF,折后BD与平面ADEF所成角正切值为
平面BCEF,折后BD与平面ADEF所成角正切值为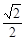 .
.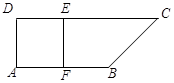
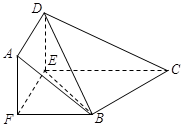
(Ⅰ)求证:
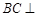 平面BDE;
平面BDE;(Ⅱ)求平面BCEF与平面ABD所成二面角(锐角)的大小.
(1)对于面面垂直的证明,主要是通过线面垂直的判定定理,以及面面垂直的判定定理来得到,属于基础题。
(2) 45°
(2) 45°
试题分析:证明(Ⅰ)∵
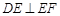 ,平面
,平面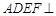 平面BCEF,∴
平面BCEF,∴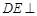 平面BCEF,
平面BCEF,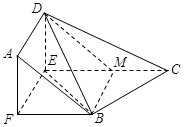
∴
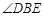 是BD与平面ADEF所成角,得
是BD与平面ADEF所成角,得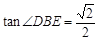 .
.设
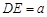 ,则
,则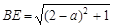 ,
,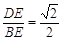 ,得
,得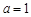 .
.∴F为AB中点,可得
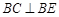 ,又
,又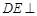 平面BCEF,得
平面BCEF,得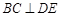 ,∴
,∴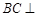 平面BDE.
平面BDE.(Ⅱ)取
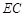 中点M,连结MB、MD,易知MB∥AD,∴平面ABMD即平面ABD.∵
中点M,连结MB、MD,易知MB∥AD,∴平面ABMD即平面ABD.∵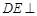 平面BCEF,∴
平面BCEF,∴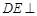 MB,∴
MB,∴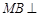 平面CDE,得,DM⊥BM.
平面CDE,得,DM⊥BM.又MB⊥EC.∴∠DME即平面BCEF与平面ABD所成二面角.
易知∠DME=45°.∴平面BCEF与平面ABD所成二面角为45°.
点评:考查了空间中垂直的证明,以及二面角的求解的运用,属于基础题。

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 ,M为线段AB的中点,N为线段DE的中点,P为线段AE的中点。
,M为线段AB的中点,N为线段DE的中点,P为线段AE的中点。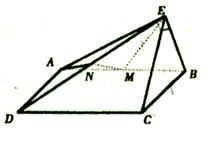
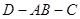 ,如图二,在二面角
,如图二,在二面角
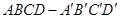 的棱长为1,O是平面
的棱长为1,O是平面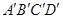 的中心,则O到平面
的中心,则O到平面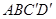 的距离是( )
的距离是( )




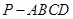 中,
中,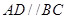 ,
,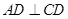 ,
,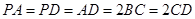 ,
,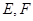 分别是
分别是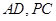 的中点.
的中点.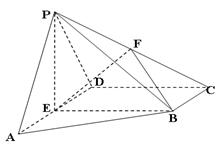
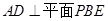 ;
;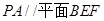 ;
;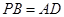 ,求二面角
,求二面角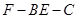 的大小.
的大小. 是三个两两不重合的平面,给出下列四个命题:
是三个两两不重合的平面,给出下列四个命题:
 ,m
,m ,则
,则 ,
,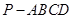 中,四边形
中,四边形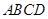 是菱形,
是菱形,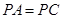 ,
,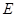 为
为 的中点.
的中点.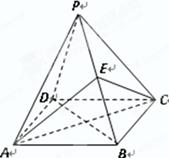
 面
面 ; (2)求证:平面
; (2)求证:平面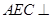 平面
平面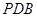 .
.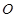 的面上有四点
的面上有四点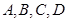 ,
,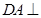 平面
平面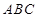 ,
,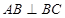 ,
,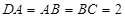 ,则球
,则球