题目内容
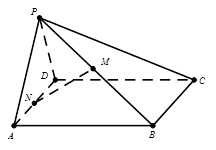
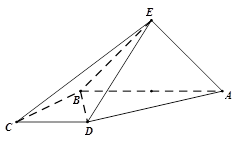
如图,边长为4的正方形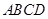 与正三角形
与正三角形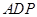 所在的平面相互垂直,且
所在的平面相互垂直,且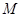 、
、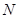
分别为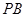 、
、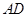 中点.
中点.
(1)求证: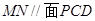 ;
;
(2)求直线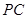 与平面
与平面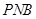 所成角的正弦值.
所成角的正弦值.
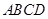 与正三角形
与正三角形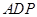 所在的平面相互垂直,且
所在的平面相互垂直,且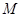 、
、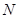
分别为
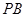 、
、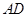 中点.
中点.
(1)求证:
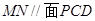 ;
;(2)求直线
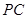 与平面
与平面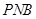 所成角的正弦值.
所成角的正弦值.(1)证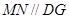 即得证. (2)
即得证. (2)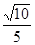
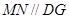 即得证. (2)
即得证. (2)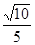
试题分析:(1)取
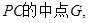 连
连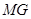 、
、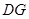 ,在
,在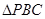 中,
中, 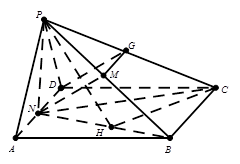
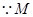 、G分别为
、G分别为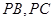 的中点,
的中点, 
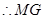 ∥
∥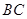 且
且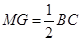 ,又
,又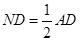 ,
,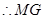
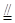
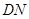 ,故四边形
,故四边形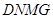 为平行四边形,
为平行四边形,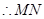 ∥
∥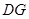 ,又
,又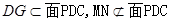 ,
,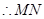 ∥
∥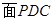
(2) 连接
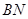 、
、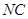 、
、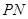 ,因为面
,因为面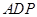
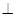 面
面 ,且
,且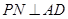 ,所以
,所以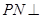 面
面 ,又
,又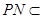 面
面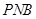 ,所以面
,所以面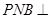 面
面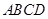 .
.过点
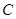 作
作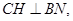 垂足为
垂足为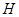 ,连
,连 ,
,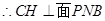 ,
,故
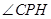
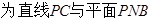 所成的角
所成的角 在正方形ABCD中,易知
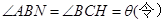 ,
,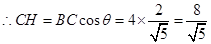
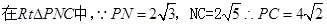 ,
,在
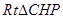 中,
中, 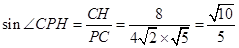
考点:与二面角有关的立体几何综合题;空间中直线与直线间的位置关系;直线与平面所成的角.
点评:本题考查异面直线垂直的证明,求二面角的大小,求直线与平面所成角的正弦值.考查运
算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综
合性强,难度大,易出错.是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
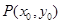
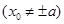 是双曲线
是双曲线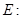
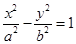
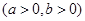 上一点,
上一点,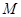 、
、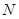 分别是双曲线
分别是双曲线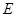 的左、右顶点,直线
的左、右顶点,直线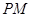 ,
, 的斜率之积为
的斜率之积为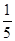 .
.
 ,
,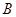 两点,
两点,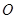 为坐标原点,
为坐标原点,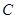 为双曲线上一点,满足
为双曲线上一点,满足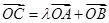 ,求
,求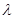 的值.
的值.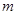 、
、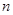 与平面
与平面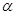 、
、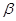 ,有下列四个命题:
,有下列四个命题: 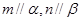 且
且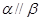 ,则
,则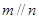 ; ②
; ②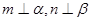 且
且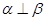 ,则
,则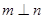 ;
;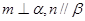 且
且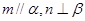 且
且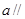 平面
平面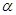 ,则
,则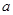 平行;
平行;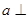 平面
平面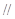 平面
平面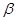 ,则
,则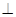 平面
平面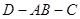 ,如图二,在二面角
,如图二,在二面角
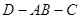 ,如图二,在二面角
,如图二,在二面角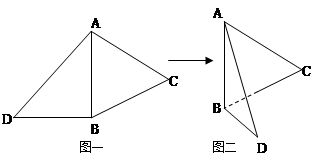
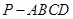 中,
中,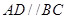 ,
,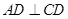 ,
,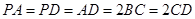 ,
,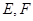 分别是
分别是 的中点.
的中点.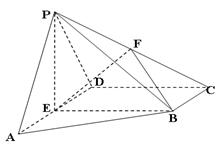
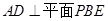 ;
;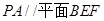 ;
;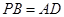 ,求二面角
,求二面角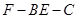 的大小.
的大小.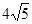
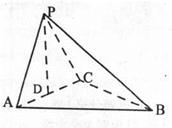
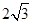 ,求二面角A-PB-C的平面角的余弦值.
,求二面角A-PB-C的平面角的余弦值. 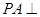 ⊙
⊙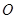 所在的平面,AB是⊙
所在的平面,AB是⊙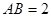 ,
,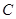 是⊙
是⊙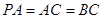 ,
,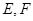 分别为
分别为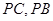 中点。
中点。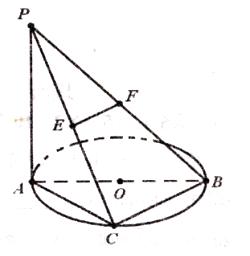
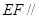 平面
平面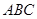 ;
;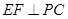 ;
; -
-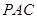 的体积。
的体积。