题目内容
设两数列{an}和{bn}，an＝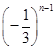
，bn＝
，则数列
的前n项的和为( )
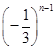，bn＝，则数列的前n项的和为( )A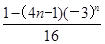． | B． |
C． | D． |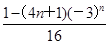
D
bn＝＝(n＋1)
＝(n＋1)[
＋…＋
]＝n.
记数列的前n项的和为Sn，则Sn＝1＋2×(－3)＋3×(－3)2＋…＋n×(－3)n－1，
－3Sn＝－3＋2×(－3)2＋3×(－3)3＋…＋n×(－3)n，
两式相减，得
4Sn＝1＋(－3)＋(－3)2＋…＋(－3)n－1－n×(－3)n＝
－n×(－3)n，故Sn＝.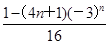
＝(n＋1)＝(n＋1)[＋…＋]＝n. 记数列
的前n项的和为Sn，则Sn＝1＋2×(－3)＋3×(－3)2＋…＋n×(－3)n－1，－3Sn＝－3＋2×(－3)2＋3×(－3)3＋…＋n×(－3)n，
两式相减，得
4Sn＝1＋(－3)＋(－3)2＋…＋(－3)n－1－n×(－3)n＝
－n×(－3)n，故Sn＝.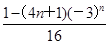
练习册系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
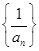是等差数列并求数列{an}的通项公式；
.
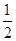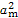=0,S2m-1=38,则m=( )
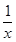(x>0)及两点A1(x1,0)和A2(x2,0)，其中x2>x1>0.过A1，A2分别作x轴的垂线，交曲线C于B1，B2两点，直线B1B2与x轴交于点A3(x3,0)，那么( )
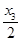，x2成等差数列
中，
，则
的值为（ ）
中，
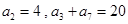，则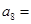
( )