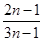题目内容
已知数列{an}满足a1=1,an-an-1+2anan-1=0(n∈N*,n>1).
(1)求证:数列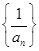 是等差数列并求数列{an}的通项公式;
是等差数列并求数列{an}的通项公式;
(2)设bn=anan+1,求证:b1+b2+…+bn<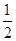 .
.
(1)求证:数列
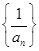 是等差数列并求数列{an}的通项公式;
是等差数列并求数列{an}的通项公式;(2)设bn=anan+1,求证:b1+b2+…+bn<
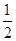 .
.(1)见解析(2)见解析
(1)已知an-an-1+2anan-1=0,两边同除以anan-1得 -
-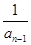 =2.
=2.
则数列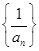 是以1为首项,2为公差的等差数列,
是以1为首项,2为公差的等差数列,
于是 =2n-1,an=
=2n-1,an=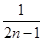 (n∈N*).
(n∈N*).
(2)由(1)知bn=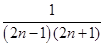 ,则
,则
b1+b2+…+bn=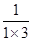 +
+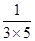 +…+
+…+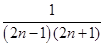 =
=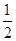 (1-
(1-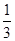 +
+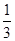 -
-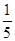 +…+
+…+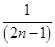 -
-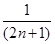 )=
)=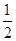 (1-
(1-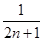 )<
)<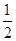
 -
-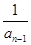 =2.
=2.则数列
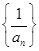 是以1为首项,2为公差的等差数列,
是以1为首项,2为公差的等差数列,于是
 =2n-1,an=
=2n-1,an=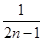 (n∈N*).
(n∈N*).(2)由(1)知bn=
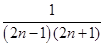 ,则
,则b1+b2+…+bn=
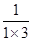 +
+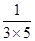 +…+
+…+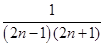 =
=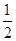 (1-
(1-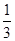 +
+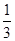 -
-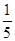 +…+
+…+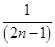 -
-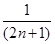 )=
)=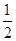 (1-
(1-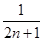 )<
)<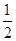

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
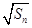 }都是等差数列,且公差相等.
}都是等差数列,且公差相等.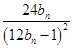 ,数列{cn}的前n项和为Tn.求证:对任意n∈N*,都有Tn<2.
,数列{cn}的前n项和为Tn.求证:对任意n∈N*,都有Tn<2.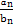 }的前n项和Sn.
}的前n项和Sn. ,
, ,-
,- ,
,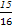 ,…的一个通项公式可以是 .
,…的一个通项公式可以是 .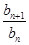 =3,n∈N*,若数列{cn}满足cn=ban,则c2 013=( )
=3,n∈N*,若数列{cn}满足cn=ban,则c2 013=( )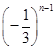 ,bn=
,bn= ,则数列
,则数列 的前n项的和为( )
的前n项的和为( )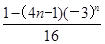


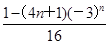
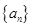 ,
,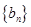 的前
的前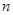 项和分别为
项和分别为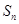 ,
,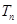 ,若
,若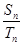
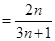 ,则
,则 ( )
( )