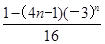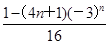题目内容
数列{an}的前n项和为Sn=4n2-n+2,则该数列的通项公式为( )
| A.an=8n-5(n∈N*) |
B.an= |
| C.an=8n+5(n≥2) |
| D.an=8n+5(n≥1) |
B
当n≥2时,an=Sn-Sn-1=4n2-n+2-[4(n-1)2-(n-1)+2]=8n-5.
当n=1时,a1=S1=5,
所以an=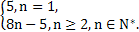
当n=1时,a1=S1=5,
所以an=
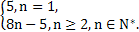

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
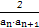 ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.
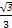
 ,
, ,-
,- ,
,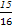 ,…的一个通项公式可以是 .
,…的一个通项公式可以是 .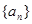 的前
的前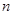 项积为
项积为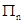 ,若
,若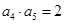 ,则
,则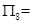 ( )
( )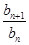 =3,n∈N*,若数列{cn}满足cn=ban,则c2 013=( )
=3,n∈N*,若数列{cn}满足cn=ban,则c2 013=( )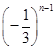 ,bn=
,bn= ,则数列
,则数列 的前n项的和为( )
的前n项的和为( )