题目内容
19.列表讨论函数y=$\frac{4(x+1)}{{x}^{2}}$-2的升降、凹凸、极值、拐点,并求出水平、垂直的切线.分析 先求导得到函数的单调性质和极值,再求导得到函数的凸凹性和拐点,由图得到切线方程.
解答  解:∵y=$\frac{4(x+1)}{{x}^{2}}$-2,
解:∵y=$\frac{4(x+1)}{{x}^{2}}$-2,
∴y′=-4($\frac{1}{{x}^{2}}$+$\frac{2}{{x}^{3}}$),
∴y″=8($\frac{1}{{x}^{3}}$+$\frac{3}{{x}^{4}}$),
| x | (-∞,-2) | -2 | (-2,0) | 0 | (0,+∞) |
| y′ | - | 极小值 | + | 极大值 | - |
| y | 单调递减 | -3 | 单调递增 | 无 | 单调递减 |
| x | (-∞,-3) | -3 | (-3,0) | 0 | (0,+∞) |
| y′ | - | 极小值 | + | - | |
| y″ | 单调递减 | $-\frac{4}{27}$ | 单调递增 | 无 | 单调递增 |
又图表和图象可知,
函数y在(-∞,-2),(0,+∞)上单调递减,在(-2,0)上单调递增,
在(-∞,0),(0,+∞)上均为凹函数,
当x=-2时有极小值,极小值为-3,无极大值,
拐点为x=-3,
水平切线为x=-3,垂直切线为x=0.
点评 本题考查了函数升降、凹凸、极值、拐点,并求出水平、垂直的切线等性质,关键是求导,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.设直线:l:y=kx+m(m≠0),双曲线C:$\frac{x^2}{16}-\frac{y^2}{9}$=1(a>0,b>0),则“k=±$\frac{3}{4}$”是“直线l与双曲线C恰有一个公共点“的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分条件 | D. | 既不充分也不必要条件 |
8.设z1,z2∈C,则“z1、z2中至少有一个数是虚数”是“z1-z2是虚数”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
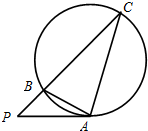 如图,过圆外一点P作圆的切线PA(A为切点),再作割线PBC依次交圆于B,C.若PA=6,PB=3,AB=4,则AC=8.
如图,过圆外一点P作圆的切线PA(A为切点),再作割线PBC依次交圆于B,C.若PA=6,PB=3,AB=4,则AC=8.