题目内容
14.设直线:l:y=kx+m(m≠0),双曲线C:$\frac{x^2}{16}-\frac{y^2}{9}$=1(a>0,b>0),则“k=±$\frac{3}{4}$”是“直线l与双曲线C恰有一个公共点“的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分条件 | D. | 既不充分也不必要条件 |
分析 根据充分条件和必要条件的定义结合直线和双曲线的位置关系进行判断即可.
解答 解:双曲线的渐近线为y=±$\frac{3}{4}$x,
当k=±$\frac{3}{4}$时,直线方程为y=±$\frac{3}{4}$x+m,m≠0与渐近线平行,此时直线l与双曲线C恰有一个公共点,即充分性成立,
当直线l与双曲线C恰有一个公共点是,k=±$\frac{3}{4}$或直线和双曲线相切,故必要性不成立,
故“k=±$\frac{3}{4}$”是“直线l与双曲线C恰有一个公共点“的充分不必要条件,
故选:A
点评 本题主要考查充分条件和必要条件的判断,利用直线和双曲线的位置关系是解决本题的关键.

练习册系列答案
相关题目
4.已知函数f(x)满足f(x+4)=f(x),且当-1<x≤3时,f(x)=$\left\{\begin{array}{l}{m\sqrt{1-{x}^{2}},x∈(-1,1]}\\{1-|x-2|,x∈(1,3]}\end{array}\right.$.其中m>0,若方程3f(x)-x=0恰好有5个根,则实数m的取值范围是( )
| A. | ($\frac{\sqrt{15}}{3}$,$\sqrt{7}$) | B. | ($\frac{\sqrt{15}}{3}$,$\frac{8}{3}$) | C. | ($\frac{4}{3}$,$\sqrt{7}$) | D. | ( $\frac{4}{3}$,$\frac{8}{3}$) |
2.某几何体的三视图如图所示,它的表面积为( )
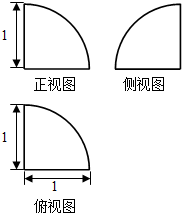

| A. | $\frac{π}{4}$ | B. | $\frac{5π}{4}$ | C. | $\frac{7π}{8}$ | D. | π |
9.甲、乙两人在2015年1月至5月的纯收入(单位:千元)的数据如下表:
(1)由表中数据直观分析,甲、乙两人中谁的纯收入较稳定?
(2)求y关于x的线性回归方程,并预测甲在6月份的纯收入;
(3)现从乙这5个月的纯收入中,随机抽取两个月,求恰有1个月的纯收入在区间(3,3.5)中的概率.
| 月份x | 1 | 2 | 3 | 4 | 5 |
| 甲的纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 |
| 乙的纯收入z | 2.8 | 3.4 | 3.8 | 4.5 | 5.5 |
(2)求y关于x的线性回归方程,并预测甲在6月份的纯收入;
(3)现从乙这5个月的纯收入中,随机抽取两个月,求恰有1个月的纯收入在区间(3,3.5)中的概率.
3.已知点A的坐标为(4$\sqrt{3}$,1),将OA绕坐标原点O逆时针旋转$\frac{π}{3}$至OB,则点B的纵坐标为( )
| A. | $\frac{{3\sqrt{3}}}{2}$ | B. | $\frac{{5\sqrt{3}}}{2}$ | C. | $\frac{11}{2}$ | D. | $\frac{13}{2}$ |
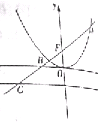 如图,过抛物线x2=2py(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=$\sqrt{2}$|BF|,且|AF|=4+2$\sqrt{2}$,则p=2.
如图,过抛物线x2=2py(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=$\sqrt{2}$|BF|,且|AF|=4+2$\sqrt{2}$,则p=2.