题目内容
11.赌博有陷阱.某种赌博每局的规则是:赌客先在标记有1,2,3,4,5的卡片中随机摸取一张,将卡片上的数字作为其赌金(单位:元);随后放回该卡片,再随机摸取两张,将这两张卡片上数字之差的绝对值的1.4倍作为其奖金(单位:元).若随机变量ξ1和ξ2分别表示赌客在一局赌博中的赌金和奖金,则 Eξ1-Eξ2=0.2(元).分析 分别求出赌金的分布列和奖金的分布列,计算出对应的均值,即可得到结论.
解答 解:赌金的分布列为
| ξ1 | 1 | 2 | 3 | 4 | 5 |
| P | $\frac{1}{5}$ | $\frac{1}{5}$ | $\frac{1}{5}$ | $\frac{1}{5}$ | $\frac{1}{5}$ |
奖金的分布列为:若两张卡片上数字之差的绝对值为1,则有(1,2),(2,3),(3,4),(4,5),4种,
若两张卡片上数字之差的绝对值为2,则有(1,3),(2,4),(3,5),3种,
若两张卡片上数字之差的绝对值为3,则有(1,4),(2,5),2种,
若两张卡片上数字之差的绝对值为4,则有(1,5),1种,
则P(ξ2=1.4)=$\frac{4}{{C}_{5}^{2}}$=$\frac{2}{5}$,P(ξ2=2.8)=$\frac{3}{{C}_{5}^{2}}$=$\frac{3}{10}$,P(ξ2=4.2)=$\frac{2}{{C}_{5}^{2}}$=$\frac{1}{5}$,P(ξ2=5.6)=$\frac{1}{{C}_{5}^{2}}$=$\frac{1}{10}$
| ξ2 | 1.4 | 2.8 | 4.2 | 5.6 |
| P | $\frac{2}{5}$ | $\frac{3}{10}$ | $\frac{1}{5}$ | $\frac{1}{10}$ |
则 Eξ1-Eξ2=3-2.8=0.2元.
故答案为:0.2
点评 本题主要考查离散型随机变量的分布列和期望的计算,根据概率的公式分别进行计算是解决本题的关键.

练习册系列答案
相关题目
1.设复数z1=-1+i,z2=$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i,则$\frac{{z}_{1}}{{z}_{2}}$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
2.某几何体的三视图如图所示,它的表面积为( )
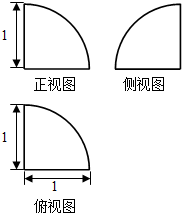

| A. | $\frac{π}{4}$ | B. | $\frac{5π}{4}$ | C. | $\frac{7π}{8}$ | D. | π |
3.已知点A的坐标为(4$\sqrt{3}$,1),将OA绕坐标原点O逆时针旋转$\frac{π}{3}$至OB,则点B的纵坐标为( )
| A. | $\frac{{3\sqrt{3}}}{2}$ | B. | $\frac{{5\sqrt{3}}}{2}$ | C. | $\frac{11}{2}$ | D. | $\frac{13}{2}$ |
10.定义运算“•”如下:x•y=$\left\{\begin{array}{l}{x,x≥y}\\{y,x<y}\end{array}\right.$,若函数f(x)=m-(1-2x)•(2x-2)有两个零点,则( )
| A. | m∈(-$\frac{1}{2}$,+∞) | B. | m∈(-$\frac{1}{2}$,1) | C. | m∈[-$\frac{1}{2}$,+∞) | D. | m∈[-$\frac{1}{2}$,1) |