题目内容
如图,△ABC是等腰直角三角形, AC=BC=a,P是△ABC所在平面外一点,PA=PB=PC= a. (1)求证:平面PAB⊥平面ABC;(2)求PC与△ABC所在平面所成的角.
a. (1)求证:平面PAB⊥平面ABC;(2)求PC与△ABC所在平面所成的角.

 a. (1)求证:平面PAB⊥平面ABC;(2)求PC与△ABC所在平面所成的角.
a. (1)求证:平面PAB⊥平面ABC;(2)求PC与△ABC所在平面所成的角. 
解: (1)证明:取AB的中点O,连结PO、CO,∵PA=PB,∴PO⊥AB,△ABC是直角三角形,∠ACB=90°,∴OA=OB=OC ∵PA=PB=PC,PO为公共边,∴△POA≌△POB≌POC
∴∠POA=∠POB=∠POC=90°,∴PO⊥CO,∴PO⊥面ABC,PO 面PAB,∴面PAB⊥面ABC
面PAB,∴面PAB⊥面ABC
(2)解:由PO⊥面ABC可知∠PCO是PC与平面ABC所成的角,∵PO=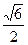 a,OC=
a,OC=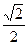 a,
a,
sinPCO=PO∶PC=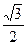 ,∴∠PCO=60°∴PC与面ABC成60°的角。
,∴∠PCO=60°∴PC与面ABC成60°的角。
∴∠POA=∠POB=∠POC=90°,∴PO⊥CO,∴PO⊥面ABC,PO
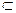 面PAB,∴面PAB⊥面ABC
面PAB,∴面PAB⊥面ABC(2)解:由PO⊥面ABC可知∠PCO是PC与平面ABC所成的角,∵PO=
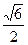 a,OC=
a,OC=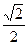 a,
a,sinPCO=PO∶PC=
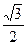 ,∴∠PCO=60°∴PC与面ABC成60°的角。
,∴∠PCO=60°∴PC与面ABC成60°的角。略

练习册系列答案
相关题目
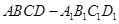 中,异面直线
中,异面直线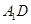 与
与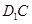 所成的角为_______度;直线
所成的角为_______度;直线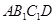 所成的角为_______度.
所成的角为_______度.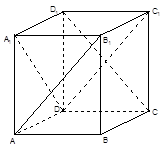
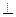 底面ABCD,E是PC的中点。
底面ABCD,E是PC的中点。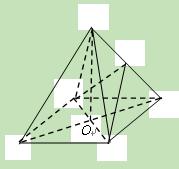

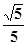
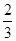





 ,则∠B= ▲ .
,则∠B= ▲ . 中,
中,
 将
将 翻折上去恰好使
翻折上去恰好使

 ;
; 试求:
试求: 的余弦值.
的余弦值. 中截面
中截面 和截面
和截面 所成的二面角的大小为( )
所成的二面角的大小为( ) B.
B. C.
C. D.
D.