题目内容
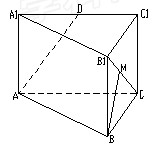
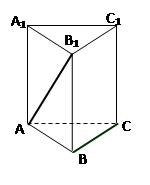
已知正三棱柱ABC-A1B1C1中,底面边长AB=2BB1,则异面直线AB1与BC所成的角的余弦值是( )

A. | B.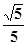 | C.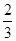 | D. |
B
分析:由正三棱柱的性质,可得异面直线AB1与BC所成的角为∠AB1C1或其补角,设B1C1=2,则 BB1 =1,△AB1C1中,由余弦定理可得cos∠AB1C1=
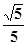 ,从而得到异面直线AB1与BC所成的角的余弦值.
,从而得到异面直线AB1与BC所成的角的余弦值.解:正三棱柱ABC-A1B1C1中,底面边长AB=2BB1,则异面直线AB1与BC所成的角为∠AB1C1或其补角,
△AB1C1中,设B1C1=2,则 BB1 =1,AC1=
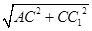 =
=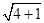 =
=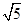 =AB1,
=AB1,△AB1C1中,由余弦定理可得 AC12=AB12+B1C12-2AB1?B1C1cos∠AB1C1,
即 5=5+4-2×
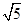 ×2cos∠AB1C1,∴cos∠AB1C1=
×2cos∠AB1C1,∴cos∠AB1C1=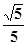 ,
,故异面直线AB1与BC所成的角的余弦值是
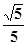
选B.

练习册系列答案
相关题目
 中,
中, 与平面
与平面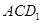 所成的角的余弦值是( )
所成的角的余弦值是( )



 中,
中, ,
, ,则面
,则面 与面
与面 所成角的为( )
所成角的为( )



 a. (1)求证:平面PAB⊥平面ABC;(2)求PC与△ABC所在平面所成的角.
a. (1)求证:平面PAB⊥平面ABC;(2)求PC与△ABC所在平面所成的角. 
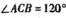 ,
,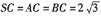 ,M
,M 为SB中点,N在AB上,满足
为SB中点,N在AB上,满足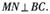
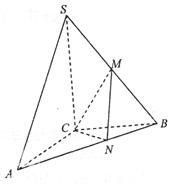





 B1C上的点M满足B1M=λB1C,若向量AD与BM的夹角小于45º,求实数λ的取值范围
B1C上的点M满足B1M=λB1C,若向量AD与BM的夹角小于45º,求实数λ的取值范围