题目内容
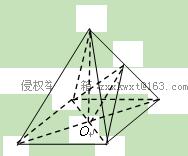
如图,O是正方形ABCD的中心,PO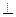 底面ABCD,E是PC的中点。
底面ABCD,E是PC的中点。
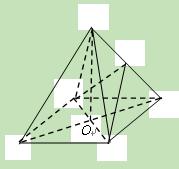
求证:(Ⅰ)PA∥平面BDE;
(Ⅱ)平面PAC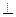 平面BDE。
平面BDE。
 底面ABCD,E是PC的中点。
底面ABCD,E是PC的中点。
求证:(Ⅰ)PA∥平面BDE;
(Ⅱ)平面PAC
 平面BDE。
平面BDE。证明:(Ⅰ)连结EO,
在△PAC中,∵O是AC的中点,E是PC的中点,
∴OE∥AP
又∵OE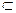 平面BDE,
平面BDE,
PA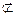 平面BDE,
平面BDE,
∴PA∥平面BDE
(Ⅱ)∵PO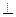 底面ABCD,
底面ABCD,
∴PO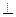 BD
BD
又∵AC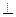 BD,且AC
BD,且AC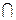 PO=O,
PO=O,
∴BD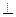 平面PAC.
平面PAC.
而BD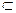 平面BDE,
平面BDE,
∴平面P AC
AC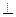 平面BDE。
平面BDE。
在△PAC中,∵O是AC的中点,E是PC的中点,

∴OE∥AP
又∵OE
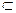 平面BDE,
平面BDE,PA
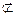 平面BDE,
平面BDE,∴PA∥平面BDE
(Ⅱ)∵PO
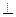 底面ABCD,
底面ABCD,∴PO
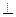 BD
BD又∵AC
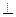 BD,且AC
BD,且AC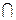 PO=O,
PO=O,∴BD
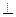 平面PAC.
平面PAC.而BD
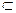 平面BDE,
平面BDE,∴平面P
 AC
AC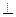 平面BDE。
平面BDE。略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
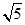 ,底面ABCD是边长为2的正方形,则CD与PA所成角的余弦值为( )
,底面ABCD是边长为2的正方形,则CD与PA所成角的余弦值为( )



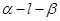 的大小为
的大小为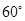 ,且
,且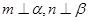 ,则异面直线m,n所成的角为( )
,则异面直线m,n所成的角为( )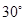
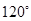
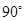
 中,
中, ,
, ,则面
,则面 与面
与面 所成角的为( )
所成角的为( )



 中,
中, ,则异面直线
,则异面直线 与
与 

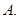

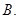





 a. (1)求证:平面PAB⊥平面ABC;(2)求PC与△ABC所在平面所成的角.
a. (1)求证:平面PAB⊥平面ABC;(2)求PC与△ABC所在平面所成的角. 

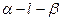 的平面角为
的平面角为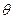 ,点
,点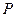 在二面角内,
在二面角内,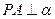 ,
,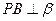 ,
,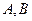 为垂足,且
为垂足,且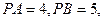 设
设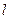 的距离分别为
的距离分别为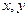 ,当
,当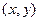 的轨迹方程是
的轨迹方程是