题目内容
已知直线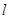 过点
过点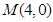 且与抛物线
且与抛物线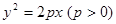 交于A、B两点,以弦AB为直径的圆恒过坐标原点O.
交于A、B两点,以弦AB为直径的圆恒过坐标原点O.
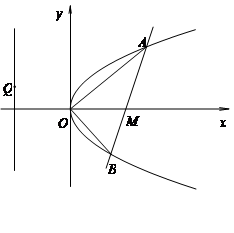
(1)求抛物线的标准方程;
(2)设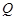 是直线
是直线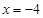 上任意一点,求证:直线QA、QM、QB的斜率依次成等差数列.
上任意一点,求证:直线QA、QM、QB的斜率依次成等差数列.
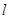 过点
过点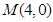 且与抛物线
且与抛物线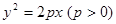 交于A、B两点,以弦AB为直径的圆恒过坐标原点O.
交于A、B两点,以弦AB为直径的圆恒过坐标原点O.
(1)求抛物线的标准方程;
(2)设
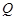 是直线
是直线 上任意一点,求证:直线QA、QM、QB的斜率依次成等差数列.
上任意一点,求证:直线QA、QM、QB的斜率依次成等差数列.(1)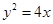 (2)详见解析.
(2)详见解析.
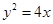 (2)详见解析.
(2)详见解析.试题分析:(1)设直线
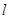 方程为
方程为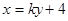 ,代入
,代入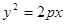 得
得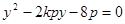
设
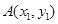 ,
,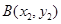 ,则有
,则有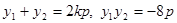 ,而
,而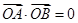 ,
,故
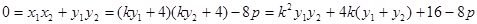
即
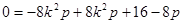 ,得
,得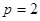 ,所以抛物线方程为
,所以抛物线方程为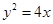 ;
;(2)由
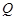 是直线
是直线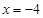 上任意一点,可设
上任意一点,可设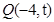 由(1)知
由(1)知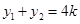 ,
,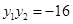 ,
,∴
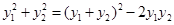 =
=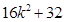 , ∵
, ∵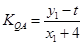 =
=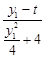 =
= ,
,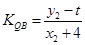 =
=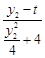 =
=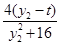 ,
,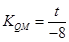
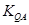 +
+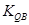 =
= +
+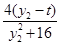 =
=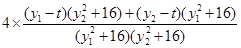
=
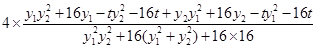 =
=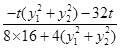 =
=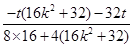 =
=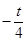 =
=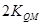 ,有等差中项的性质可知直线QA、QP、QB的斜率依次成等差数列.
,有等差中项的性质可知直线QA、QP、QB的斜率依次成等差数列.试题解析:(1)设直线
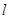 方程为
方程为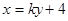 ,代入
,代入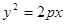 得
得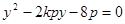
设
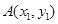 ,
,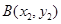 ,则有
,则有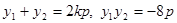 2分
2分
而
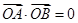 ,
,故
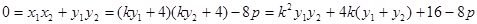
即
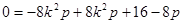 ,得
,得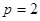 ,所以抛物线方程为
,所以抛物线方程为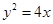 6分
6分说明:取过M 点的特殊位置的直线求得抛物线的方程给满分.
(2)设
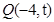 由(1)知
由(1)知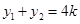 ,
,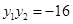 ,
,∴
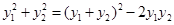 =
=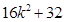 , ∵
, ∵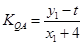 =
=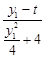 =
= ,
,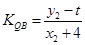 =
=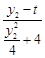 =
=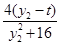 ,
,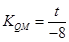 9分
9分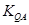 +
+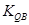 =
= +
+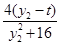 =
=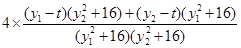
=
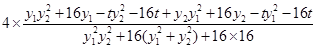
=
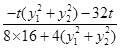 =
=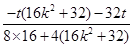 =
=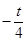 =
=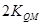 12分
12分所以直线QA、QP、QB的斜率依次成等差数列. 13分

练习册系列答案
相关题目

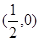

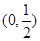
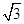 ,那么|PF|=________.
,那么|PF|=________. y,过点A(0,-1)和点B(t,3)的直线与抛物线C没有公共点,则实数t的取值范围是( ).
y,过点A(0,-1)和点B(t,3)的直线与抛物线C没有公共点,则实数t的取值范围是( ). ∪
∪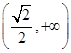
 ∪(2
∪(2 ,+∞)
,+∞) ∪
∪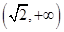
 ,则其标准方程为_______.
,则其标准方程为_______.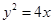 的焦点为
的焦点为 ,准线为直线
,准线为直线 ,过抛物线上一点
,过抛物线上一点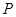 作
作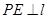 于
于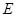 ,若直线
,若直线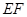 的倾斜角为
的倾斜角为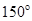 ,则
,则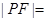 ______.
______. 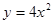 的焦点坐标是( )
的焦点坐标是( )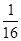 )
)