题目内容
设抛物线y2=8x的焦点为F,准线为l,P为抛物线上一点PA⊥l,A为垂足,如果AF的斜率为-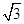 ,那么|PF|=________.
,那么|PF|=________.
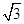 ,那么|PF|=________.
,那么|PF|=________.8
抛物线的焦点为F(2,0),准线为x=-2,因为PA⊥准线l,设P(m,n),则A(-2,n),因为AF的斜率为-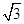 ,所以
,所以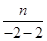 =
=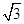 ,得n=-4
,得n=-4 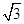 ,点P在抛物线上,所以8m=(-4
,点P在抛物线上,所以8m=(-4 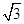 )2=48,m=6.因此P(6,-4
)2=48,m=6.因此P(6,-4 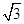 ),|PF|=|PA|=|6-(-2)|=8.
),|PF|=|PA|=|6-(-2)|=8.
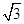 ,所以
,所以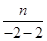 =
=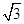 ,得n=-4
,得n=-4 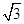 ,点P在抛物线上,所以8m=(-4
,点P在抛物线上,所以8m=(-4 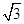 )2=48,m=6.因此P(6,-4
)2=48,m=6.因此P(6,-4 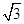 ),|PF|=|PA|=|6-(-2)|=8.
),|PF|=|PA|=|6-(-2)|=8.
练习册系列答案
相关题目
 过点
过点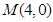 且与抛物线
且与抛物线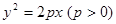 交于A、B两点,以弦AB为直径的圆恒过坐标原点O.
交于A、B两点,以弦AB为直径的圆恒过坐标原点O.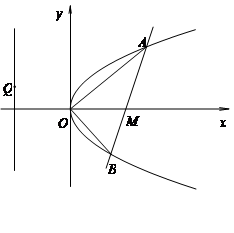
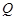 是直线
是直线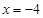 上任意一点,求证:直线QA、QM、QB的斜率依次成等差数列.
上任意一点,求证:直线QA、QM、QB的斜率依次成等差数列.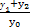 的值为 .
的值为 .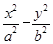 =1(a>0,b>0)的两条渐近线围成一个等腰直角三角形,则该双曲线的离心率是( )
=1(a>0,b>0)的两条渐近线围成一个等腰直角三角形,则该双曲线的离心率是( )
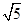
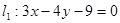 和直线
和直线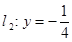 ,抛物线
,抛物线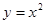 上一动点
上一动点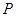 到直线
到直线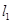 和直线
和直线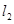 的距离之和的最小值是 。
的距离之和的最小值是 。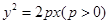 的焦点的距离是5,那么P= .
的焦点的距离是5,那么P= .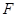 是抛物线
是抛物线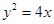 的焦点,点
的焦点,点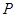 在该抛物线上,且点
在该抛物线上,且点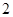 ,则
,则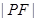 =( )
=( )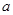 ,则M到y轴距离为 ( )
,则M到y轴距离为 ( )