Question

【题目】已知中心在坐标原点的椭圆与双曲线有公共焦点，且左、右焦点分别为，．这两条曲线在第一象限的交点为，是以为底边的等腰三角形．若，记椭圆与双曲线的离心率分别为、，则的取值范围是_____．

Answer 1

【答案】

【解析】

如图所示，设椭圆与双曲线的标准方程分别为：，．（a1，a2，b1，b2＞0，a1＞b1）．根据△PF1F2是以PF1为底边的等腰三角形，|PF1|＝10，可得10+2c＝2a1，10﹣2c＝2a2，可得，于是e1+e2＝e2f（e2），e2＞1．利用导数研究其单调性即可得出．

解：如图所示，

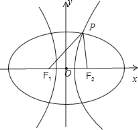
设椭圆与双曲线的标准方程分别为：，．（a1，a2，b1，b2＞0，a1＞b1）

∵△PF1F2是以PF1为底边的等腰三角形，|PF1|＝10，

∴10+2c＝2a1，10﹣2c＝2a2，

相减可得：2c＝a1﹣a2，

∴，

∴，

∴e1+e2＝e2f（e2），e2＞1．

∴f′（e2）＝110，

∴函数f（e2）在e2＞1时单调递增，

∴f（e2）＞f（1）＝1．

∴e1+e2的取值范围是．

故答案为：．