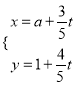题目内容
【题目】已知函数
为二次函数，不等式
的解集是
，且在区间
上的最大值为12．
（1）求的解析式；
（2）设函数在
上的最小值为
，求的表达式及的最小值．
【答案】（1）
．（2）
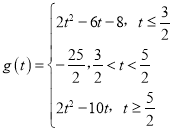.最小值
【解析】
(1)根据
是二次函数，且
的解集是
可设出的零点式,再根据在区间
上的最大值在对称轴处取得为12即可算出对应的参数.
(2)由(1)求得
后改写成顶点式,再根据对称轴与区间的位置关系,分情况进行讨论即可.
（1）是二次函数，且的解集是，
∴可设
，
可得在区间在区间
上函数是减函数，区间
上函数是增函数．
∵
，
，
，
∴在区间上的最大值是
，得
．
因此，函数的表达式为．
（2）由（1）得
，函数图象的开口向上，对称轴为
，
①当
时，即
时，在
上单调递减，
此时的最小值
；
②当
时，在上单调递增，
此时的最小值
；
③当
时，函数
在对称轴处取得最小值，
此时，
，
综上所述，得
的表达式为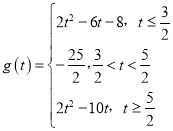
，
当
，取最小值
练习册系列答案
53随堂测系列答案
相关题目
