题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,判断
时,判断![]() 是否为
是否为![]() 的极值点,并说明理由;
的极值点,并说明理由;
(2)记![]() .若函数
.若函数![]() 存在极大值
存在极大值![]() ,证明:
,证明:![]() .
.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)将![]() 代入可得
代入可得![]() ,即
,即![]() ,对函数
,对函数![]() 进行求导,令
进行求导,令![]() ,再次进行求导,通过
,再次进行求导,通过![]() 与0的关系,得到
与0的关系,得到![]() 的单调性及最小值为0,即
的单调性及最小值为0,即![]() 恒成立,可得结果;(2)求导可得
恒成立,可得结果;(2)求导可得![]() ,对
,对![]() 进行讨论,分为
进行讨论,分为![]() ,
,![]() ,
,![]() 和
和![]() 四种情形,判断单调性得极值,得其极值
四种情形,判断单调性得极值,得其极值![]() ,再求出
,再求出![]() 的最值即可.
的最值即可.
试题解析:(1)由![]() ,可得
,可得![]() ,故
,故![]() .
.
![]() 不是
不是![]() 的极值点.
的极值点.
理由如下:![]() .
.
记![]() ,则
,则![]() .
.
由![]() ,解得
,解得![]() ;由
;由![]() ,解得
,解得![]() ,
,
所以![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
故![]()
![]() ,即
,即![]() 在
在![]() 恒单调递增,
恒单调递增,
故![]() 不是
不是![]() 的极值点.
的极值点.
(2)依题意,![]() .
.
则![]() .
.
①![]() 时,
时,![]() 在
在![]() 恒成立,
恒成立,![]() 在
在![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上先减后增,故
上先减后增,故![]() 在
在![]() 上有极小值,无极大值,应舍去.
上有极小值,无极大值,应舍去.
②![]() 时,
时,![]() 在
在![]() 恒成立,
恒成立,![]() 在
在![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上先减后增,故
上先减后增,故![]() 在
在![]() 上有极小值,无极大值,应舍去.
上有极小值,无极大值,应舍去.
③![]() 时,由
时,由![]() 得
得![]() 和
和![]() ,
,
|
|
| |
| 大于 | 小于 | 大于 |
| 单调递增 | 单调递减 | 单调递增 |
因为![]() ,故有下列对应关系表:
,故有下列对应关系表:
故![]() ,
,
记![]() ,
,
因为![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() .
.
④当![]() 时,因为
时,因为![]() ,故
,故
|
|
| |
| 大于 | 小于 | 大于 |
| 单调递增 | 单调递减 | 单调递增 |
故![]() ,
,
设![]() ,
,
记![]() ,
,
则![]() ,令
,令![]() 得
得![]() 和
和![]() (舍去),
(舍去),
|
| |
| 小于 | 大于 |
| 单调递减 | 单调递增 |
故![]() .
.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
【题目】某市2011年至2017年新开楼盘的平均销售价格(单位:千元/平方米)的统计数据如下表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售价格 | 3 | 3.4 | 3.7 | 4.5 | 4.9 | 5.3 | 6 |
(1)求![]() 关于x的线性回归方程;
关于x的线性回归方程;
(2)利用(1)中的回归方程,分析2011年至2017年该市新开楼盘平均销售价格的变化情况,并预测该市2019年新开楼盘的平均销售价格。
附:参考公式: 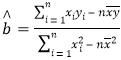 ,
,![]() ,其中
,其中![]() 为样本平均值。
为样本平均值。
参考数据:![]()
![]() .
.