题目内容
【题目】命题![]() :指数函数
:指数函数![]() 是减函数;命题
是减函数;命题![]() :
:![]() ,使关于
,使关于![]() 的方程
的方程![]() 有实数解,其中
有实数解,其中![]() .
.
(1)当![]() 时,若
时,若![]() 为真命题,求
为真命题,求![]() 的取值范围;
的取值范围;
(2)当![]() 时,若
时,若![]() 且
且![]() 为假命题,求
为假命题,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)当![]() 时,根据指数函数的单调性,即可求得实数
时,根据指数函数的单调性,即可求得实数![]() 的取值范围为
的取值范围为![]() .
.
(2)当![]() 时,根据指数函数的性质和一元二次方程的性质,分别求得命题
时,根据指数函数的性质和一元二次方程的性质,分别求得命题![]() 为真命题时,实数
为真命题时,实数![]() 的取值范围,进而分类讨论,得到
的取值范围,进而分类讨论,得到![]() 且
且![]() 为假命题时,实数
为假命题时,实数![]() 的取值范围。
的取值范围。
(1)当![]() 时,指数函数
时,指数函数![]() 化为
化为![]()
因为指数函数![]() 是减函数,所以
是减函数,所以![]()
即![]()
所以实数![]() 的取值范围为
的取值范围为![]() .
.
(2)当![]() 时,指数函数
时,指数函数![]() 化为
化为![]()
若命题![]() 为真命题,则
为真命题,则![]() ,即
,即![]()
所以![]() 为假命题时
为假命题时![]() 的取值范围是
的取值范围是![]() 或
或![]()
命题![]() 为真命题时,即关于
为真命题时,即关于![]() 的方程
的方程![]() 有实数解,
有实数解,
所以![]() ,解得
,解得![]() ,
,
所以命题![]() 为假命题时
为假命题时![]() 的取值范围为
的取值范围为![]()
因为![]() 且
且![]() 为假命题,所以
为假命题,所以![]() 为假命题或者
为假命题或者![]() 为假命题
为假命题
所以实数![]() 满足
满足![]() 或
或![]() 或
或![]() ,即
,即![]() 或
或![]()
所以实数![]() 的取值范围为
的取值范围为![]()

 阅读快车系列答案
阅读快车系列答案【题目】某市2011年至2017年新开楼盘的平均销售价格(单位:千元/平方米)的统计数据如下表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售价格 | 3 | 3.4 | 3.7 | 4.5 | 4.9 | 5.3 | 6 |
(1)求![]() 关于x的线性回归方程;
关于x的线性回归方程;
(2)利用(1)中的回归方程,分析2011年至2017年该市新开楼盘平均销售价格的变化情况,并预测该市2019年新开楼盘的平均销售价格。
附:参考公式: 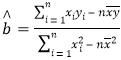 ,
,![]() ,其中
,其中![]() 为样本平均值。
为样本平均值。
参考数据:![]()
![]() .
.
【题目】从某食品厂生产的面包中抽取![]() 个,测量这些面包的一项质量指标值,由测量结果得如下频数分布表:
个,测量这些面包的一项质量指标值,由测量结果得如下频数分布表:
质量指标值分组 |
|
|
|
|
|
频数 |
|
|
|
|
|

(1)在相应位置上作出这些数据的频率分布直方图;
(2)估计这种面包质量指标值的平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(3)根据以上抽样调查数据,能否认为该食品厂生产的这种面包符合“质量指标值不低于![]() 的面包至少要占全部面包
的面包至少要占全部面包![]() 的规定?”
的规定?”
