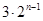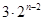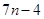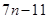��Ŀ����
��֪����B1(1,y1)��B2(2,y2)������Bn(n,yn)��n��N�� ˳��Ϊһ�κ���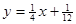 ͼ���ϵĵ㣬 ����A1(x1,0)��A2(x2,0)������An(xn,0)��n��N�� ˳��Ϊx���������ϵĵ㣬����x1=a��0��a��1���� ��������n��N����An��Bn��An+1������ BnΪ����ĵ���������.
ͼ���ϵĵ㣬 ����A1(x1,0)��A2(x2,0)������An(xn,0)��n��N�� ˳��Ϊx���������ϵĵ㣬����x1=a��0��a��1���� ��������n��N����An��Bn��An+1������ BnΪ����ĵ���������.
����{yn}��ͨ�ʽ����֤��{yn}�ǵȲ����У�
�����ж�xn+2-xn�Ƿ�Ϊͬһ����������֤���������������{xn}��ͨ�ʽ��
������������������AnBnAn+1�У��Ƿ����ֱ�������Σ����У������ʱaֵ���������ڣ� ��˵������.
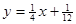 ͼ���ϵĵ㣬 ����A1(x1,0)��A2(x2,0)������An(xn,0)��n��N�� ˳��Ϊx���������ϵĵ㣬����x1=a��0��a��1���� ��������n��N����An��Bn��An+1������ BnΪ����ĵ���������.
ͼ���ϵĵ㣬 ����A1(x1,0)��A2(x2,0)������An(xn,0)��n��N�� ˳��Ϊx���������ϵĵ㣬����x1=a��0��a��1���� ��������n��N����An��Bn��An+1������ BnΪ����ĵ���������.����{yn}��ͨ�ʽ����֤��{yn}�ǵȲ����У�
�����ж�xn+2-xn�Ƿ�Ϊͬһ����������֤���������������{xn}��ͨ�ʽ��
������������������AnBnAn+1�У��Ƿ����ֱ�������Σ����У������ʱaֵ���������ڣ� ��˵������.
��1��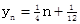 (nÎN)����2��xn=
(nÎN)����2��xn=
��3������ֱ�����Σ���ʱa��ֵΪ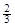 ��
��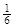 ��
��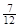 .
.
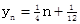 (nÎN)����2��xn=
(nÎN)����2��xn=
��3������ֱ�����Σ���ʱa��ֵΪ
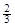 ��
��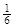 ��
��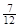 .
. ��I����Ϊ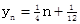 (nÎN),���ݵȲ����еĶ����жϳ�{yn}Ϊ�Ȳ�����.
(nÎN),���ݵȲ����еĶ����жϳ�{yn}Ϊ�Ȳ�����.
��II���ⱾС��Ĺؼ����ȸ���xn+1-xn=2Ϊ����,��ȷ��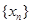 ���������ż����ֱ�ɵȲ����У��Ӷ����
���������ż����ֱ�ɵȲ����У��Ӷ����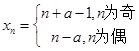 .
.
(III) ҪʹAnBnAn+1Ϊֱ�����Σ��� |AnAn+1|=2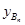 =2(
=2(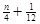 )Þxn+1-xn=2(
)Þxn+1-xn=2(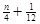 )��
)��
��nΪ����ʱ��xn+1-xn=2(1-a)����nΪż��ʱ��xn+1-xn=2a.Ȼ��ֱ��о�����.
��1��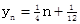 (nÎN),yn+1-yn=
(nÎN),yn+1-yn=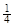 ,��{yn}Ϊ�Ȳ����� (4¢)
,��{yn}Ϊ�Ȳ����� (4¢)
��2��xn+1-xn=2Ϊ���� (6¢) ��x1,x3,x5,��,x2n-1��x2,x4,x6,,����x2n���ǹ���Ϊ2�ĵȲ����У�
��x2n-1=x1+2(n-1)=2n-2+a��x2n=x2+2(n-1)=2-a+2n-2=2n-a��
��xn=
��3��ҪʹAnBnAn+1Ϊֱ�����Σ��� |AnAn+1|=2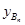 =2(
=2(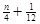 )Þxn+1-xn=2(
)Þxn+1-xn=2(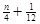 )
)
��nΪ����ʱ��xn+1=n+1-a��xn=n+a-1,��xn+1-xn=2(1-a).
Þ2(1-a)=2(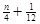 ) Þa=
) Þa=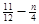 (nΪ������0��a��1) (*)
(n������0��a��1) (*)
ȡn=1����a=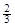 ��ȡn=3����a=
��ȡn=3����a=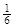 ����n��5����(*)�⣻ (14¢)
����n��5����(*)�⣻ (14¢)
��ż��ʱ��xn+1=n+a��xn=n-a����xn+1-xn=2a.
��2a=2(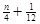 )Þa=
)Þa=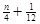 (nΪż����0��a��1) (*¢)��ȡn=2����a=
(nΪż����0��a��1) (*¢)��ȡn=2����a=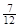 ,
,
��n��4����(*¢)��.
���Ͽ�֪������ֱ�����Σ���ʱa��ֵΪ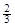 ��
��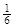 ��
��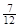 . (18¢)
. (18¢)
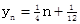 (nÎN),���ݵȲ����еĶ����жϳ�{yn}Ϊ�Ȳ�����.
(nÎN),���ݵȲ����еĶ����жϳ�{yn}Ϊ�Ȳ�����.��II���ⱾС��Ĺؼ����ȸ���xn+1-xn=2Ϊ����,��ȷ��
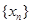 ���������ż����ֱ�ɵȲ����У��Ӷ����
���������ż����ֱ�ɵȲ����У��Ӷ����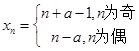 .
.(III) ҪʹAnBnAn+1Ϊֱ�����Σ��� |AnAn+1|=2
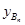 =2(
=2(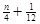 )Þxn+1-xn=2(
)Þxn+1-xn=2(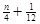 )��
)����nΪ����ʱ��xn+1-xn=2(1-a)����nΪż��ʱ��xn+1-xn=2a.Ȼ��ֱ��о�����.
��1��
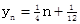 (nÎN),yn+1-yn=
(nÎN),yn+1-yn=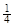 ,��{yn}Ϊ�Ȳ����� (4¢)
,��{yn}Ϊ�Ȳ����� (4¢)��2��xn+1-xn=2Ϊ���� (6¢) ��x1,x3,x5,��,x2n-1��x2,x4,x6,,����x2n���ǹ���Ϊ2�ĵȲ����У�
��x2n-1=x1+2(n-1)=2n-2+a��x2n=x2+2(n-1)=2-a+2n-2=2n-a��
��xn=

��3��ҪʹAnBnAn+1Ϊֱ�����Σ��� |AnAn+1|=2
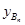 =2(
=2(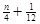 )Þxn+1-xn=2(
)Þxn+1-xn=2(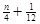 )
)��nΪ����ʱ��xn+1=n+1-a��xn=n+a-1,��xn+1-xn=2(1-a).
Þ2(1-a)=2(
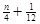 ) Þa=
) Þa=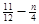 (nΪ������0��a��1) (*)
(nΪ������0��a��1) (*)ȡn=1����a=
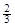 ��ȡn=3����a=
��ȡn=3����a=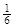 ����n��5����(*)�⣻ (14¢)
����n��5����(*)�⣻ (14¢)��ż��ʱ��xn+1=n+a��xn=n-a����xn+1-xn=2a.
��2a=2(
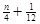 )Þa=
)Þa=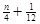 (nΪż����0��a��1) (*¢)��ȡn=2����a=
(nΪż����0��a��1) (*¢)��ȡn=2����a=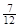 ,
,��n��4����(*¢)��.
���Ͽ�֪������ֱ�����Σ���ʱa��ֵΪ
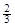 ��
��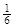 ��
��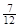 . (18¢)
. (18¢)
��ϰ��ϵ�д�
 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
�����Ŀ
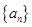 ���㣺
���㣺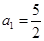 ����
����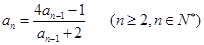
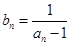 ��֤������
��֤������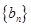 �ǵȲ����У���2��������
�ǵȲ����У���2��������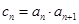 ��
��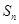 ����
Ϊ����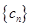 ��ǰ
��ǰ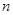 ��ͣ�֤��
��ͣ�֤��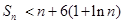 .
. �У�
��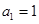 ��
��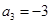 ��
�� ���
��� ����
����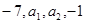 �ĸ�ʵ���ɵȲ����У���4��b1��b2��b3����1���ʵ���ɵȱ����У���
�ĸ�ʵ���ɵȲ����У���4��b1��b2��b3����1���ʵ���ɵȱ����У���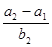 = �� ��
= �� �� 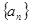 ��ǰ
��ǰ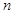 ���
���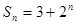 ��������
��������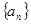 ��ǰn��ĺ�Sn = 2n2-n+1����an=
��ǰn��ĺ�Sn = 2n2-n+1����an= 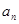 }�ǵȲ����У�
}�ǵȲ����У�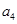 =7����
=7���� =_________
=_________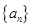 ����
�У���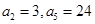 ����ͨ��
����ͨ��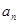 = ( )
= ( )