题目内容
已知数列{xn}的首项x1=3,通项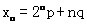 (n∈N+,p、q为常数)且x1,x4,x5成等差数列.
(n∈N+,p、q为常数)且x1,x4,x5成等差数列.
(Ⅰ)求p、q的值; (Ⅱ){xn}前n项和为Sn,计算S10的值.
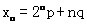 (n∈N+,p、q为常数)且x1,x4,x5成等差数列.
(n∈N+,p、q为常数)且x1,x4,x5成等差数列. (Ⅰ)求p、q的值; (Ⅱ){xn}前n项和为Sn,计算S10的值.
(Ⅰ) p=1,q=1 (Ⅱ) 2101
本试题主要是考查了等差数列的性质的运用和数列求和问题。
(1)由x1=3,则3="2p+q"
又x1,x4,x5成等差数列,则(3+32p+5q)=2(16p+4q) 联立得到。
(2)因此S10=2+22+…+210+1+2+…+10=2101
解:(1)由x1=3,则3=2p+q ①
又x1,x4,x5成等差数列,则(3+32p+5q)=2(16p+4q) ②
联①②得p=1,q=1,xn=2n+n.
(2)S10=2+22+…+210+1+2+…+10=2101.
(1)由x1=3,则3="2p+q"
又x1,x4,x5成等差数列,则(3+32p+5q)=2(16p+4q) 联立得到。
(2)因此S10=2+22+…+210+1+2+…+10=2101
解:(1)由x1=3,则3=2p+q ①
又x1,x4,x5成等差数列,则(3+32p+5q)=2(16p+4q) ②
联①②得p=1,q=1,xn=2n+n.
(2)S10=2+22+…+210+1+2+…+10=2101.

练习册系列答案
相关题目
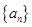 满足:
满足: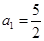 ,且
,且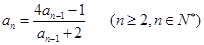
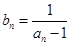 ,证明数列
,证明数列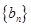 是等差数列;(2)求数列
是等差数列;(2)求数列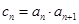 ,
,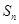 为数列
为数列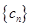 的前
的前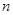 项和,证明
项和,证明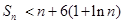 .
. 和等比数列
和等比数列 中,a1=2b1=2,b6=32,
中,a1=2b1=2,b6=32,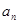 和
和 ;
;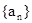 前n项的和
前n项的和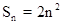 ,数列
,数列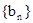 为等比数列,
为等比数列,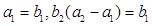 .
.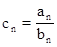 ,求
,求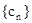 的前n项和
的前n项和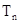 .
. 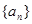 满足:
满足: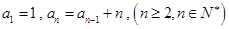 .
.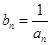 ,求数列
,求数列 的前
的前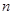 项和
项和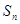 .
.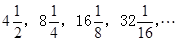 ,的前
,的前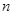 项和为( )
项和为( )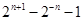
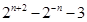

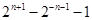
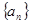 中,设
中,设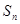 为前
为前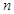 项和,且
项和,且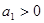 ,
,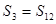 ,当
,当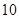

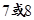

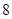
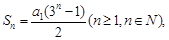 且a4=54,则a1= .
且a4=54,则a1= .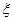 的分布列为,
的分布列为,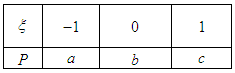
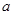 、
、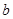 、
、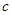 成等差数列,若
成等差数列,若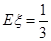 ,则
,则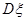 =
=