题目内容
【题目】如图,已知点E是圆心为O1半径为2的半圆弧上从点B数起的第一个三等分点,点F是圆心为O2半径为1的半圆弧的中点,AB、CD分别是两个半圆的直径,O1O2=2,直线O1O2与两个半圆所在的平面均垂直,直线AB、DC共面.
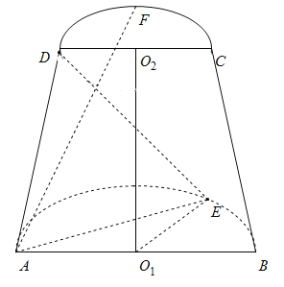
(1)求三棱锥D﹣ABE的体积;
(2)求直线DE与平面ABE所成的角的正切值;
(3)求直线AF与BE所成角的余弦值.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
![]() 由题意知,
由题意知,![]() 即为所求三棱锥的高,代入三棱锥的体积公式
即为所求三棱锥的高,代入三棱锥的体积公式![]() 求解即可;
求解即可;
![]() 以O1为坐标原点,
以O1为坐标原点,![]() ,
,![]() ,
,![]() 分别为x、y、z轴的正向,建立空间直角坐标系如图所示,利用空间向量法分别求出面ABE的法向量
分别为x、y、z轴的正向,建立空间直角坐标系如图所示,利用空间向量法分别求出面ABE的法向量![]() 和向量
和向量![]() 的坐标,向量
的坐标,向量![]() 与向量
与向量![]() 的夹角余弦即为直线DE与平面ABE所成的角的正弦值,进而求出正切值即可;
的夹角余弦即为直线DE与平面ABE所成的角的正弦值,进而求出正切值即可;
![]() 以O1为坐标原点,
以O1为坐标原点,![]() ,
,![]() ,
,![]() 分别为x、y、z轴的正向,建立空间直角坐标系如图所示,利用空间向量法,向量
分别为x、y、z轴的正向,建立空间直角坐标系如图所示,利用空间向量法,向量![]() 所成角的余弦值的绝对值即为所求.
所成角的余弦值的绝对值即为所求.
(1)∵![]() ,O1E=2,
,O1E=2,
∴![]() ,
,
∵直线O1O2与两个半圆所在的平面均垂直,直线AB、DC共面,
∴三棱锥D﹣ABE的高等于O1O2=2,
所以![]() .
.
(2)以O1为坐标原点,![]() ,
,![]() ,
,![]() 分别为x、y、z轴的正向
分别为x、y、z轴的正向
建立空间直角坐标系如图所示:
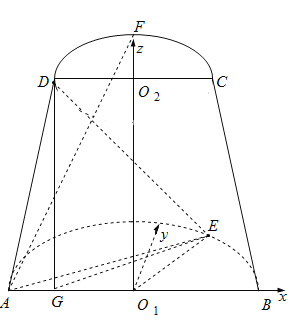
则,D(-1,0,2),E![]() ,
,
![]() ,
,
由题意可知,平面ABE的一个法向量为![]() (0,0,1),
(0,0,1),
设直线DE与平面ABE所成的角为θ,
则sinθ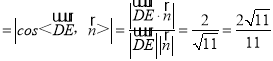 ,
,
因为![]() .∴
.∴![]() ,
,
所以![]() 即为所求.
即为所求.
(3)以O1为坐标原点,![]() ,
,![]() ,
,![]() 分别为x、y、z轴的正向,
分别为x、y、z轴的正向,
建立空间直角坐标系如图所示:

则A(﹣2,0,0),B(2,0,0),E![]() ,F(0,1,2),
,F(0,1,2),
所以![]() (2,1,2),
(2,1,2),![]() ,
,
设直线AF与BE所成角为θ,
则cosθ .
.
∴直线AF与BE所成角的余弦值为![]() .
.

【题目】为了研究玉米品种对产量的 ,某农科院对一块试验田种植的一批玉米共10000株的生长情况进行研究,现采用分层抽样方法抽取50株作为样本,统计结果如下:
高茎 | 矮茎 | 总计 | |
圆粒 | 11 | 19 | 30 |
皱粒 | 13 | 7 | 20 |
总计 | 24 | 26 | 50 |
(1)现采用分层抽样的方法,从该样本所含的圆粒玉米中取出6株玉米,再从这6株玉米中随机选出2株,求这2株之中既有高茎玉米又有矮茎玉米的概率;
(2)根据玉米生长情况作出统计,是否有95%的把握认为玉米的圆粒与玉米的高茎有关?
附: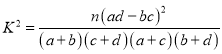
| 0.05 | 0.01 |
| 3.841 | 6.635 |
【题目】前些年有些地方由于受到提高![]() 的影响,部分企业只重视经济效益而没有树立环保意识,把大量的污染物排放到空中与地下,严重影响了人们的正常生活,为此政府进行强制整治,对不合格企业进行关闭,整顿,另一方面进行大量的绿化来净化和吸附污染物,通过几年的整治,环境明显得到好转,针对政府这一行为,老百姓大大点赞.
的影响,部分企业只重视经济效益而没有树立环保意识,把大量的污染物排放到空中与地下,严重影响了人们的正常生活,为此政府进行强制整治,对不合格企业进行关闭,整顿,另一方面进行大量的绿化来净化和吸附污染物,通过几年的整治,环境明显得到好转,针对政府这一行为,老百姓大大点赞.
(1)某机构随机访问50名居民,这50名居民对政府的评分(满分100分)如下表:
分数 |
|
|
|
|
|
|
频数 | 2 | 3 | 11 | 14 | 11 | 9 |
请在答题卡上作出居民对政府的评分频率分布直方图:
(2)当地环保部门随机抽测了2019年6月的空气质量指数,其数据如下表:
空气质量指数 | 0—50 | 50—100 | 100—150 | 150—200 |
天数 | 2 | 18 | 8 | 2 |
用空气质量指数的平均值作为该月空气质量指数级别,求出该月空气质量指数级别为第几级?(同一组数据用该组数据的区间中点值作代表,将频率视为概率)(相关知识参见附表)
(3)空气受到污染,呼吸系统等疾病患者最易感染,根据历史经验,凡遇到空气轻度污染,小李每天会服用有关药品花费50元,遇到中度污染每天服药的费用达到100元.环境整治前的2015年11月份小李因受到空气污染患呼吸系统等疾病花费了5000元,试估计2019年11月份(参考(2)中表格数据)小李比以前少花了多少钱的医药费?
附:
空气质量指数 | 0-50 | 50-100 | 100-150 | 150-200 | 200-300 | >300 |
空气质量指数级别 | I | II | III | IV | V | VI |
空气质量指数 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |