题目内容
【题目】△ABC为等腰直角三角形,AC=BC=4,∠ACB=90°,D、E分别是边AC和AB的中点,现将△ADE沿DE折起,使面ADE⊥面DEBC,H、F分别是边AD和BE的中点,平面BCH与AE、AF分别交于I、G两点
(Ⅰ)求证:IH∥BC;
(Ⅱ)求直线AE与平面角GIC所成角的正弦值.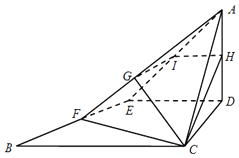
【答案】(I)证明:DE∥BC,DE平面BCH,BC平面BCH,∴DE∥平面BCH,
∵平面ADE∩平面BCH=IH,
∴DE∥IH,
∴IH∥BC.
(II)解:建立如图所示的空间直角坐标系.
D(0,0,0),A(0,0,2),E(0,﹣2,0),C(2,0,0),
H(0,0,1),B(2,﹣4,0),![]() =(﹣2,0,1),
=(﹣2,0,1), ![]() =(0,﹣4,0),
=(0,﹣4,0), ![]() =(0,﹣2,﹣2).
=(0,﹣2,﹣2).
设平面BCH的法向量为 ![]() =(x,y,z),则
=(x,y,z),则  ,即
,即 ![]() ,取
,取 ![]() =(1,0,2).
=(1,0,2).
设直线AE与平面角GIC所成角为θ,则sinθ=|cos ![]() |=
|=  =
= ![]() =
= ![]() .
.
【解析】(Ⅰ)DE∥BC,可得DE∥平面BCH,可得DE∥IH,即可证明IH∥BC.(Ⅱ)建立如图所示的空间直角坐标系.设平面BCH的法向量为 ![]() =(x,y,z),则
=(x,y,z),则  ,设直线AE与平面角GIC所成角为θ,则sinθ=|cos
,设直线AE与平面角GIC所成角为θ,则sinθ=|cos ![]() |=
|=  .
.
【考点精析】通过灵活运用直线与平面平行的性质和空间角的异面直线所成的角,掌握一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行;简记为:线面平行则线线平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 即可以解答此题.
即可以解答此题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目