题目内容
【题目】已知函数 ![]() 是偶函数,直线y=t与函数y=f(x)的图象自左向右依次交于四个不同点A,B,C,D.若AB=BC,则实数t的值为 .
是偶函数,直线y=t与函数y=f(x)的图象自左向右依次交于四个不同点A,B,C,D.若AB=BC,则实数t的值为 .
【答案】﹣ ![]()
【解析】解:因为f(x)是偶函数,所以x>0时恒有f(﹣x)=f(x),即x2﹣bx+c=ax2﹣2x﹣1, 所以(a﹣1)x2+(b﹣2)x﹣c﹣1=0,
所以 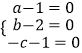 ,解得a=1,b=2,c=﹣1,
,解得a=1,b=2,c=﹣1,
所以f(x)= ![]() ,
,
由t=x2+2x﹣1,即x2+2x﹣1﹣t=0,解得x=﹣1± ![]() ,
,
故xA=﹣1﹣ ![]() ,xB=﹣1+
,xB=﹣1+ ![]() ,
,
由t=x2﹣2x﹣1,即x2﹣2x﹣1﹣t=0,解得x=1± ![]() ,
,
故xC=1﹣ ![]() ,
,
因为AB=BC,所以xB﹣xA=xC﹣xB , 即2 ![]() =2﹣2
=2﹣2 ![]() ,解得t=﹣
,解得t=﹣ ![]() ,
,
所以答案是:﹣ ![]() .
.
【考点精析】解答此题的关键在于理解函数的奇偶性的相关知识,掌握偶函数的图象关于y轴对称;奇函数的图象关于原点对称,以及对函数的零点的理解,了解函数的零点就是方程的实数根,亦即函数的图象与轴交点的横坐标.即:方程有实数根,函数的图象与坐标轴有交点,函数有零点.

练习册系列答案
相关题目