题目内容
【题目】在平面直角坐标系![]() 中,设点
中,设点![]() (1,0),直线
(1,0),直线![]() :
: ![]() ,点
,点![]() 在直线
在直线![]() 上移动,
上移动, ![]() 是线段
是线段![]() 与
与![]() 轴的交点, 异于点R的点Q满足:
轴的交点, 异于点R的点Q满足: ![]() ,
, ![]() .
.
(1)求动点![]() 的轨迹的方程;
的轨迹的方程;
(2) 记![]() 的轨迹的方程为
的轨迹的方程为![]() ,过点
,过点![]() 作两条互相垂直的曲线
作两条互相垂直的曲线![]()
的弦![]() .
. ![]() ,设
,设![]() .
. ![]() 的中点分别为
的中点分别为![]() .
.
问直线![]() 是否经过某个定点?如果是,求出该定点,
是否经过某个定点?如果是,求出该定点,
如果不是,说明理由.
【答案】(Ⅰ) ![]() ;(Ⅱ)以直线
;(Ⅱ)以直线![]() 恒过定点
恒过定点![]()
![]() .
.
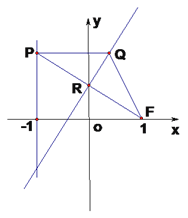
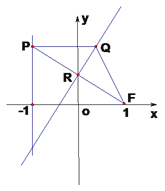
【解析】试题分析: (1)由已知条件知,点R是线段FP的中点,RQ是线段FP的垂直平分线,点Q的轨迹E是以F为焦点,l为准线的抛物线,写出抛物线标准方程.
(2)设出直线AB的方程,把A、B坐标代入抛物线方程,再利用中点公式求出点M的坐标,同理可得N的坐标,求出直线MN的斜率,得到直线MN的方程并化简,可看出直线MN过定点.
试题解析:(Ⅰ)依题意知,直线![]() 的方程为:
的方程为: ![]() .点
.点![]() 是线段
是线段![]() 的中点,
的中点,
且![]() ⊥
⊥![]() ,∴
,∴![]() 是线段
是线段![]() 的垂直平分线.
的垂直平分线.
∴![]() 是点
是点![]() 到直线
到直线![]() 的距离.
的距离.
∵点![]() 在线段
在线段![]() 的垂直平分线,∴
的垂直平分线,∴![]() .
.
故动点![]() 的轨迹
的轨迹![]() 是以
是以![]() 为焦点,
为焦点, ![]() 为准线的抛物线,
为准线的抛物线,
其方程为: ![]() .
.
(Ⅱ) 设![]() ,
, ![]() ,
,
由AB⊥CD,且AB、CD与抛物线均有两个不同的交点,故直线AB、CD斜率均存在,设直线AB的方程为![]()
则
(1)—(2)得![]() ,即
,即![]() ,
,
代入方程![]() ,解得
,解得![]() .所以点M的坐标为
.所以点M的坐标为![]() .
.
同理可得: ![]() 的坐标为
的坐标为![]() .
.
直线![]() 的斜率为
的斜率为![]() ,方程为
,方程为
![]() ,整理得
,整理得![]() ,
,
显然,不论![]() 为何值,
为何值, ![]() 均满足方程,所以直线
均满足方程,所以直线![]() 恒过定点
恒过定点![]()
![]() .
.

练习册系列答案
相关题目