题目内容
【题目】(本小题满分16分)
设数列![]() 的前
的前![]() 项的和为
项的和为![]() ,已知
,已知![]() .
.
⑴求![]() ,
,![]() 及
及![]() ;
;
⑵设![]() ,若对一切
,若对一切![]() ,均有
,均有![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
【答案】(1)Sn=n(n+1)(n∈N+),(2)m<0或m≥5
【解析】试题分析:根据数列题中![]() 的前
的前![]() 项和与前
项和与前![]() 项和作差求出
项和作差求出![]() ,再利用
,再利用![]() 求出
求出![]() ,从而写出
,从而写出![]() ,判断
,判断![]() 为等比数列,利用等比数列的求和公式求出前
为等比数列,利用等比数列的求和公式求出前![]() 项和,根据单调型求出
项和,根据单调型求出![]() 的范围,再根据题意求出
的范围,再根据题意求出![]() 的范围.
的范围.
试题解析:
(1)依题意,n=1时,S1=2,n=2时,S2=6,
∵![]() ,①
,①
n≥2时, ![]() ,②
,②
①﹣②,得![]() ,
,
∴Sn=n(n+1)(n∈N+),
(2)由(1)知Sn=n(n+1),
当n≥2时,an=Sn﹣Sn﹣1=2n,
∵a1=2,∴an=2n,n∈N+,
∴![]() .
.
∵![]() ,∴数列{bn}是等比数列,
,∴数列{bn}是等比数列,
则 b1+b2+…+bn=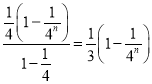 .
.
∵![]() 随n的增大而增大,
随n的增大而增大,
∴![]() b1+b2+…+bn
b1+b2+…+bn![]() ,
,
因为![]() ,
,
则依条件,得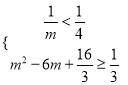 ,
,
即![]() ,∴m<0或m≥5
,∴m<0或m≥5

练习册系列答案
相关题目