题目内容
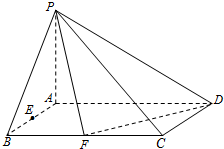 已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.(Ⅰ)判断并说明PA上是否存在点G,使得EG∥平面PFD?若存在,求出
| PG |
| GA |
(Ⅱ)若PB与平面ABCD所成的角为45°,求二面角A-PD-F的平面角的余弦值.
考点:二面角的平面角及求法,直线与平面平行的性质
专题:平面向量及应用,空间角
分析:(Ⅰ)首先假设点的存在,建立空间直角坐标系利用法向量建立向量间的关系.
(Ⅱ)利用线面的夹角,和法向量,求出夹角的余弦值.
(Ⅱ)利用线面的夹角,和法向量,求出夹角的余弦值.
解答:
 解:(Ⅰ)假设在PA上存在点G,使得EG∥平面
解:(Ⅰ)假设在PA上存在点G,使得EG∥平面
PFD,建立如图所示的空间直角坐标系,设PA=a,GA=b.
∵F(1,1,0),D(0,2,0),P(0,0,a),G(0,0,b),
∴
=(1,-1,0),
=(0,2,-a),
=(
,0,-b).
设平面PFD的一个法向量
=(x,a,z).
∵
,
∴
,
∴
=(a,a,2).
∵
•
=
a-2b=0,
∴b=
a.
∴
=3.
PA上存在点G,使得EG∥平面PFD.
(Ⅱ)∵∠PBA为直线PB与平面ABCD所成的角,
所以:∠PBA=45°
∵AB=1
∴PA=1
由(Ⅰ)得:平面PDF的法向量为:
=(1,1,2)
平面APD的法向量为:
=(1,0,0)
由于:cos<
>=
所以:二面角A-PD-F的平面角的余弦值
.
 解:(Ⅰ)假设在PA上存在点G,使得EG∥平面
解:(Ⅰ)假设在PA上存在点G,使得EG∥平面PFD,建立如图所示的空间直角坐标系,设PA=a,GA=b.
∵F(1,1,0),D(0,2,0),P(0,0,a),G(0,0,b),
∴
| DF |
| PD |
| GE |
| 1 |
| 2 |
设平面PFD的一个法向量
| m |
∵
|
∴
|
∴
| m |
∵
| GE |
| m |
| 1 |
| 2 |
∴b=
| 1 |
| 4 |
∴
| PG |
| GE |
PA上存在点G,使得EG∥平面PFD.
(Ⅱ)∵∠PBA为直线PB与平面ABCD所成的角,
所以:∠PBA=45°
∵AB=1
∴PA=1
由(Ⅰ)得:平面PDF的法向量为:
| m |
平面APD的法向量为:
| n |
由于:cos<
| m, |
| n |
| ||
| 6 |
所以:二面角A-PD-F的平面角的余弦值
| ||
| 6 |
点评:本题考查的知识要点:存在性问题的应用,二面角的应用.法向量的应用,空间直角坐标系的建立,属于基础题型.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 抛物线有光学性质,从焦点出发的光经抛物线反射后沿平行于抛物线的对称轴方向射出,今有抛物线y2=2px(p>0),一光源在点A(6,4)处,由其发出的光线沿平行于抛物线的对称轴的方向射向抛物线上的B点,反射后,又射向抛物线上的C点,再反射后沿平行于抛物线的对称轴的方向射出,途中遇到直线l:x-y-7=0上的点D,再反射后又射回到A点,如图所示,则此抛物线的方程为( )
抛物线有光学性质,从焦点出发的光经抛物线反射后沿平行于抛物线的对称轴方向射出,今有抛物线y2=2px(p>0),一光源在点A(6,4)处,由其发出的光线沿平行于抛物线的对称轴的方向射向抛物线上的B点,反射后,又射向抛物线上的C点,再反射后沿平行于抛物线的对称轴的方向射出,途中遇到直线l:x-y-7=0上的点D,再反射后又射回到A点,如图所示,则此抛物线的方程为( )| A、y2=2x |
| B、y2=4x |
| C、y2=8x |
| D、y2=16x |
已知f(x)=ax2+bx+c,且b>0,若对任意x有f(x)≥0,则
的最小值为( )
| f(1) |
| b |
| A、3 | ||
B、
| ||
| C、2 | ||
D、
|
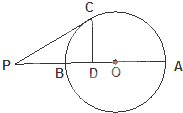 如图:AB是⊙O的直径,点P在AB的延长线上,且PB=OB=2,PC切⊙O于点C,CD⊥AB于点D,则CD=
如图:AB是⊙O的直径,点P在AB的延长线上,且PB=OB=2,PC切⊙O于点C,CD⊥AB于点D,则CD=