题目内容
已知函数f(x)=x+
(a>0)
(1)判断函数f(x)在(0,+∞)的单调性;
(2)若f(x)=x+
在(0,4)上是减函数,在(4,+∞)上是增函数,求实数b的值;
(3)若c∈[1,4],求函数f(x)=x+
在区间[1,2]上的最大值和最小值.
| a |
| x |
(1)判断函数f(x)在(0,+∞)的单调性;
(2)若f(x)=x+
| 2b |
| x |
(3)若c∈[1,4],求函数f(x)=x+
| c |
| x |
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:计算题,分类讨论,导数的综合应用
分析:(1)求出导数,令导数大于0,得增区间,令导数小于0,得减区间;
(2)运用基本不等式,结合条件可得,
=4,解得b,即可;
(3)运用基本不等式,可得当x=
时,f(x)取得最小值f(
)=2
,讨论当1≤c≤2时,当c=2时,当2<c≤4时,求得最大值即可.
(2)运用基本不等式,结合条件可得,
| 2b |
(3)运用基本不等式,可得当x=
| c |
| c |
| c |
解答:
解:(1)∵f′(x)=1-
∴当x>0时,由f′(x)>0可解得x>
,
由f′(x)<0可解得0<x<
,
∴函数f(x)在(0,
)上是减函数,在(
,+∞)上是增函数;
(2)f(x)=x+
(x>0)≥2
,当且仅当x=
,取得最小值,
∵2b>0∴由题意可知
=4,故b=4;
(3)∵1≤c≤4∴1≤
≤2,
∴函数f(x)在[1,
]上是减函数,在(
,2]上是增函数,
故当x=
时,f(x)取得最小值f(
)=2
又∵f(1)=1+c,f(2)=2+
,
∴当1≤c≤2时,f(x)的最大值为f(2)=2+
,
当c=2时,f(x)的最大值为f(1)=f(2)=3,
当2<c≤4时,f(x)的最大值为f(1)=1+c.
| a |
| x2 |
∴当x>0时,由f′(x)>0可解得x>
| a |
由f′(x)<0可解得0<x<
| a |
∴函数f(x)在(0,
| a |
| a |
(2)f(x)=x+
| 2b |
| x |
| 2b |
| 2b |
∵2b>0∴由题意可知
| 2b |
(3)∵1≤c≤4∴1≤
| c |
∴函数f(x)在[1,
| c |
| c |
故当x=
| c |
| c |
| c |
又∵f(1)=1+c,f(2)=2+
| c |
| 2 |
∴当1≤c≤2时,f(x)的最大值为f(2)=2+
| c |
| 2 |
当c=2时,f(x)的最大值为f(1)=f(2)=3,
当2<c≤4时,f(x)的最大值为f(1)=1+c.
点评:本题考查导数的运用:求单调区间,考查函数的单调性和运用:求最值和范围,考查分类讨论的思想方法,考查运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
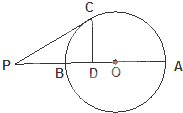 如图:AB是⊙O的直径,点P在AB的延长线上,且PB=OB=2,PC切⊙O于点C,CD⊥AB于点D,则CD=
如图:AB是⊙O的直径,点P在AB的延长线上,且PB=OB=2,PC切⊙O于点C,CD⊥AB于点D,则CD=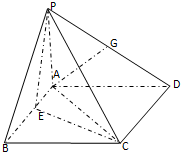 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,A点在PD上的射影为G点,E点在AB上,平面PEC⊥平面PDC.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,A点在PD上的射影为G点,E点在AB上,平面PEC⊥平面PDC.