题目内容
已知点P(4,3),保持点P与原点的距离不变,并绕原点分别旋转45°、120°、-45°到P1、P2、P3的位置,求点P1、P2、P3的坐标.
考点:任意角的三角函数的定义
专题:计算题,三角函数的求值
分析:求出|OP|=
=5,设∠xOP=θ,则sinθ=
,cosθ=
,再求θ+45°,θ+120°,θ-45°的正弦和余弦,再由坐标公式x=rcosθ,y=rsinθ,即可得到所求点的坐标.
| 32+42 |
| 3 |
| 5 |
| 4 |
| 5 |
解答:
解:|OP|=
=5,设∠xOP=θ,则sinθ=
,cosθ=
,
则cos(θ+45°)=
(cosθ-sinθ)=
,sin(θ+45°)=
(cosθ+sinθ)=
,
则有P1(
,
);
cos(θ+120°)=-
cosθ-
sinθ=-
,sin(θ+120°)=-
sinθ+
cosθ=
,
则有P2(-
,
);
cos(θ-45°)=
(cosθ+sinθ)=
,sin(θ-45°)=
(sinθ-cosθ)=-
,
则有P3(
,-
).
即有有P1(
,
),P2(-
,
),有P3(
,-
).
| 32+42 |
| 3 |
| 5 |
| 4 |
| 5 |
则cos(θ+45°)=
| ||
| 2 |
| ||
| 10 |
| ||
| 2 |
7
| ||
| 10 |
则有P1(
| ||
| 2 |
7
| ||
| 2 |
cos(θ+120°)=-
| 1 |
| 2 |
| ||
| 2 |
4+3
| ||
| 10 |
| 1 |
| 2 |
| ||
| 2 |
4
| ||
| 10 |
则有P2(-
4+3
| ||
| 2 |
4
| ||
| 2 |
cos(θ-45°)=
| ||
| 2 |
7
| ||
| 10 |
| ||
| 2 |
| ||
| 10 |
则有P3(
7
| ||
| 2 |
| ||
| 5 |
即有有P1(
| ||
| 2 |
7
| ||
| 2 |
4+3
| ||
| 2 |
4
| ||
| 2 |
7
| ||
| 2 |
| ||
| 5 |
点评:本题考查任意角的三角函数的定义和两角和差的正弦和余弦公式的运用,考查运算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
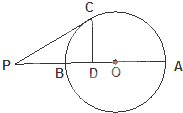 如图:AB是⊙O的直径,点P在AB的延长线上,且PB=OB=2,PC切⊙O于点C,CD⊥AB于点D,则CD=
如图:AB是⊙O的直径,点P在AB的延长线上,且PB=OB=2,PC切⊙O于点C,CD⊥AB于点D,则CD=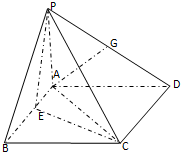 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,A点在PD上的射影为G点,E点在AB上,平面PEC⊥平面PDC.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,A点在PD上的射影为G点,E点在AB上,平面PEC⊥平面PDC.