题目内容
5.执行如图所示的程序框图,则输出的S值是( )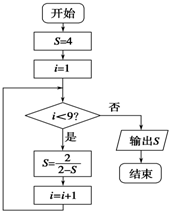
| A. | -1 | B. | $\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | 4 |
分析 计算i=1,2,3,4,5发现每4次一个循环,得到i=8时输出S.
解答 解:由已知程序框图得到①i=1,S=-1;
②i=2,S=$\frac{2}{3}$;③i=3,S=$\frac{3}{2}$;
④i=4,S=4;
⑤i=5,S=-1…
所以i=8时与i=4时的S值相等;
故选:D.
点评 本题考查了程序框图中,循环结构的执行次数与输出值;关键是读懂框图,明确执行结束时的i值.

练习册系列答案
相关题目
15.设A、B是两个集合,则“A∩B=A”是“A⊆B”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
13.函数f(x)的定义域为D,对给定的正数k,若存在闭区间[a,b]⊆D,使得函数f(x)满足:①f(x)在[a,b]内是单调函数;②f(x)在[a,b]上的值域为[ka,kb],则称区间[a,b]为y=f(x)的k级“理想区间”.下列结论错误的是( )
| A. | 函数f(x)=-x2(x∈R)存在1级“理想区间” | |
| B. | 函数f(x)=ex(x∈R)不存在2级“理想区间” | |
| C. | 函数f(x)=$\frac{4x}{{x}^{2}+1}$(x≥0)存在3级“理想区间” | |
| D. | 函数f(x)=loga(ax-$\frac{1}{4}$)(a>0,a≠1)不存在4级“理想区间” |
20.已知直线y=$\frac{1}{3}x+\frac{2}{3}$与幂函数f(x)=xm(m≠0)的图象将于A、B两点,且|AB|=$\sqrt{10}$,则m的值为( )
| A. | -2 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
14.现有10张奖券,其中8张2元,2张5元,今某人随机无放回的抽取三张,则此人得奖金金额的数学期望为( )
| A. | 6元 | B. | 12元 | C. | 7.8元 | D. | 9元 |