题目内容
13.函数f(x)的定义域为D,对给定的正数k,若存在闭区间[a,b]⊆D,使得函数f(x)满足:①f(x)在[a,b]内是单调函数;②f(x)在[a,b]上的值域为[ka,kb],则称区间[a,b]为y=f(x)的k级“理想区间”.下列结论错误的是( )| A. | 函数f(x)=-x2(x∈R)存在1级“理想区间” | |
| B. | 函数f(x)=ex(x∈R)不存在2级“理想区间” | |
| C. | 函数f(x)=4xx2+14xx2+1(x≥0)存在3级“理想区间” | |
| D. | 函数f(x)=loga(ax-1414)(a>0,a≠1)不存在4级“理想区间” |
分析 A、B、C中,可以找出定义域中的“理想区间”,从而作出正确的选择.D中,假设存在“理想区间”[a,b],会得出错误的结论.
解答 解:A中,当x≥0时,f(x)=-x2在[0,1]上是单调减函数,且f(x)在[0,1]上的值域是[0,1],∴存在1级“理想区间”,原命题正确;
B中,当x∈R时,f(x)=ex在[a,b]上是单调增函数,且f(x)在[a,b]上的值域是[ea,eb,],∴不存在2级“理想区间”,原命题正确;
C中,因为f(x)=4xx2+14xx2+1=4x+1x4x+1x在(0,1)上为增函数.假设存在[a,b]?(0,1),使得f(x)∈[3a,3b]则有{f(a)=3af(b)=3b,所以命题正确;
D中,若函数(a>0,a≠1).不妨设a>1,则函数在定义域内为单调增函数,
若存在“4级理想区间”[m,n],
则由,得即m,n是方程loga(ax-14)=4x的两个根,
即m,n是方程a4x-ax+14=0的两个根,
由于该方程有两个不等的正根,故存在“4级理想区间”[m,n],∴D结论错误
故选:D.
点评 本题考查了新定义下的函数的性质与应用问题,解题时应理解新定义中的题意与要求,转化为解题的条件与结论,是易错题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
3.设函数f′(x)是奇函数f(x)(x∈R)的导函数,f(-1)=0,当x>0时,xf′(x)-f(x)<0,则使得f(x)>0成立的x的取值范围是( )
| A. | (-∞,-1)∪(0,1) | B. | (-1,0)∪(1,+∞) | C. | (-∞,-1)∪(-1,0) | D. | (0,1)∪(1,+∞) |
1.随着三星S6手机的上市,很多消费者觉得价格偏高,尤其是大部分学生可望而不可及,因此我市沃尔玛“三星手机专卖店”推出无抵押分期付款购买方式,该店对最近100名采用分期付款的购买者进行统计,统计结果如下表所示:
已知分3期付款的频率为0.15,并且店销售一部三星S6,顾客分1期付款,其利润为1000元;分2期或3期付款,其利润为1500元;分4期或5期付款,其利润为2000元,以频率作为概率.以此样本估计总体,试解决以下问题
(Ⅰ)求事件A:“购买的3位顾客中,恰好有1名顾客分4期付款”的概率;
(Ⅱ)用X表示销售一部三星S6手机的利润,求X的分布列及数学期望.
| 付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频 数 | 35 | 25 | a | 10 | b |
(Ⅰ)求事件A:“购买的3位顾客中,恰好有1名顾客分4期付款”的概率;
(Ⅱ)用X表示销售一部三星S6手机的利润,求X的分布列及数学期望.
18.若直线ax+by=4与不等式组{2x−5y+8≥02x+y−4≤0x+2y+4≥0表示的平面区域无公共点,则a+b的取值范围( )
| A. | (32,3) | B. | (-3,3) | C. | (-3,32) | D. | (-1,3) |
5.执行如图所示的程序框图,则输出的S值是( )
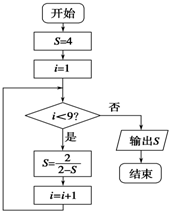

| A. | -1 | B. | 23 | C. | 32 | D. | 4 |
2.给出两个命题:命题p:不等式0<α<π成立是不等式sinα>0成立的必要不充分条件;命题q:函数y=log2(√x2+1-x)是奇函数,则下列命题是真命题的是( )
| A. | p∧q | B. | p∨¬q | C. | p∨q | D. | p∧¬q |
3.如图,函数f(x)的图象为折线ACB,则不等式f(x)≥log2(x+1)的解集是( )


| A. | {x|-1<x≤0} | B. | {x|-1≤x≤1} | C. | {x|-1<x≤1} | D. | {x|-1<x≤2} |
