题目内容
16.若实数a,b,c成等差数列,点P(-1,0)在动直线ax+by+c=0上的射影为点M,已知点N(3,3),则线段MN的最大值与最小值的和为10.分析 由a,b,c成等差数列,利用等差数列的性质得到2b=a+c,整理后与直线方程ax+by+c=0比较发现,直线ax+by+c=0恒过Q(1,-2),再由点P(-1,0)在动直线ax+by+c=0上的射影为M,得到PM与QM垂直,利用圆周角定理得到M在以PQ为直径的圆上,由P和Q的坐标,利用中点坐标公式求出圆心A的坐标,利用两点间的距离公式求出此圆的半径r,线段MN长度的最大值即为M与圆心A的距离与半径的和,求出即可
解答 解:∵a,b,c成等差数列,
∴2b=a+c,即a-2b+c=0,
可得方程ax+by+c=0恒过Q(1,-2),
又点P(-1,0)在动直线ax+by+c=0上的射影为M,
∴∠PMQ=90°,
∴M在以PQ为直径的圆上,
∴此圆的圆心A坐标为($\frac{1-1}{2}$,$\frac{-2+0}{2}$),即A(0,-1),半径r=$\frac{1}{2}$|PQ|=$\frac{1}{2}$$\sqrt{(1+1)^{2}+(-2)^{2}}$=$\sqrt{2}$,
又N(3,3),
∴|AN|=5,
则|MN|max=5+$\sqrt{2}$,最小值为5-$\sqrt{2}$,所以线段MN的最大值与最小值的和为10.
故答案为:10.
点评 此题考查了等差数列的性质,恒过定点的直线方程,圆周角定理,线段中点坐标公式,以及两点间的距离公式,利用等差数列的性质得到2b=a+c,即a-2b+c=0是解本题的突破点.

练习册系列答案
相关题目
6.设$\overrightarrow{a}$,$\overrightarrow{b}$是非零向量,“$\overrightarrow{a}•\overrightarrow{b}$=|$\overrightarrow{a}$||$\overrightarrow{b}$|”是“$\overrightarrow{a}$$∥\overrightarrow{b}$”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
1.随着三星S6手机的上市,很多消费者觉得价格偏高,尤其是大部分学生可望而不可及,因此我市沃尔玛“三星手机专卖店”推出无抵押分期付款购买方式,该店对最近100名采用分期付款的购买者进行统计,统计结果如下表所示:
已知分3期付款的频率为0.15,并且店销售一部三星S6,顾客分1期付款,其利润为1000元;分2期或3期付款,其利润为1500元;分4期或5期付款,其利润为2000元,以频率作为概率.以此样本估计总体,试解决以下问题
(Ⅰ)求事件A:“购买的3位顾客中,恰好有1名顾客分4期付款”的概率;
(Ⅱ)用X表示销售一部三星S6手机的利润,求X的分布列及数学期望.
| 付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频 数 | 35 | 25 | a | 10 | b |
(Ⅰ)求事件A:“购买的3位顾客中,恰好有1名顾客分4期付款”的概率;
(Ⅱ)用X表示销售一部三星S6手机的利润,求X的分布列及数学期望.
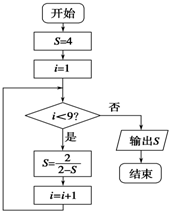
5.执行如图所示的程序框图,则输出的S值是( )

| A. | -1 | B. | $\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | 4 |
6.已知等腰直角三角形的直角边的长为2,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )
| A. | $\frac{2\sqrt{2}π}{3}$ | B. | $\frac{4\sqrt{2}π}{3}$ | C. | 2$\sqrt{2}$π | D. | 4$\sqrt{2}$π |
 如图,在⊙O中,相交于点E的两弦AB,CD的中点分别是M,N,直线MO与直线CD相交于点F,证明:
如图,在⊙O中,相交于点E的两弦AB,CD的中点分别是M,N,直线MO与直线CD相交于点F,证明: